
已知函数 在
在 上单调递减且满足
上单调递减且满足 .
.
(1)求 的取值范围.
的取值范围.
(2)设 ,求
,求 在
在 上的最大值和最小值.
上的最大值和最小值.
(1)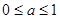 ;(2)当
;(2)当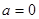 时,
时, 在
在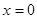 取得最小值
取得最小值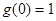 ,
,
在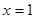 上取得最大值
上取得最大值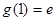 .
.
当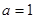 时,
时,  在
在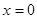 取得最大值
取得最大值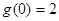 ,在
,在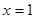 时取得最小值
时取得最小值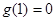 .
.
当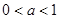 时,由
时,由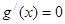 ,得
,得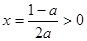 .
.
当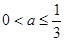 时,
时, 在
在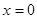 时取得最小值
时取得最小值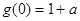 ,在
,在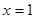 时取得最大值
时取得最大值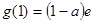 .
.
当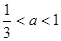 时,
时, 在
在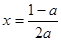 时取得最大值
时取得最大值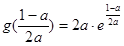 ,在
,在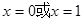 时取得最小值,
时取得最小值,
当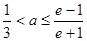 时,
时, 在
在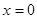 时取得最小值
时取得最小值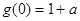 ;
;
当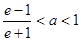 时,
时, 在
在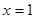 时取得最小值
时取得最小值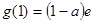 .
.
解析试题分析:(1)注意到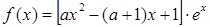 ,
,
其导函数为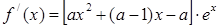
根据题意得到“对于任意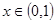 .有
.有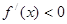 ”.所以结合二次函数的性质分类讨论.
”.所以结合二次函数的性质分类讨论.
具体情况有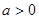 ,
,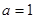 ,
, 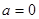 ,
,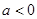 .
.
(2)注意到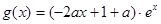 ,
,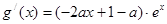 ,
,
讨论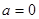 ,
,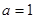 ,
,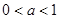 的情况.
的情况.
而在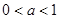 时,要结合二次函数的图象和性质,具体地讨论①若
时,要结合二次函数的图象和性质,具体地讨论①若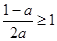 ,即
,即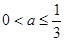 ;
;
②若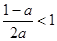 ,即
,即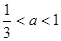 的不同情况.
的不同情况.
易错点在于分类讨论不全面.
试题解析:
(1)由 得:
得: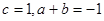
则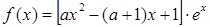 ,
,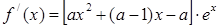
依题意需对于任意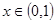 .有
.有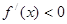 .
.
当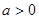 时,因为二次函数
时,因为二次函数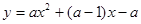 的图像开口向上,
的图像开口向上,
而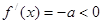 ,所以需
,所以需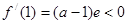 ,即
,即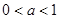 ;
;
当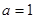 时,对任意
时,对任意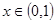 有
有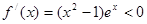 ,
, 符合条件;
符合条件;
当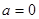 时,对任意
时,对任意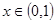 有
有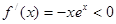 ,
, 符合条件;
符合条件;
当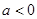 时,因为
时,因为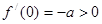 ,
, 不符合条件.
不符合条件.
故 的取值范围为
的取值范围为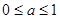 .
.
(2)因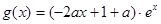 ,
,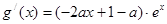 ,
,
当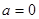 时,
时,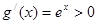 ,
, 在
在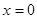 取得最小值
取得最小值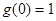 ,
,
在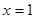 上取得最大值
上取得最大值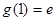 .
.
当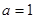 时,对任意
时,对任意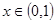 有
有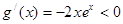 ,
, 在
在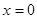 取得最大值
取得最大值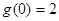 ,在
,在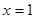 时取得最小值
时取得最小值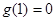 .
.
当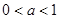 时,由
时,由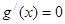 ,得
,得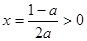 .
.
①若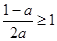 ,即
,即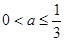 时,
时, 在
在 上单调递增,
上单调递增, 在
在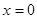 时取得最小值
时取得最小值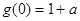 ,在
,在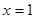 时取得最大值
时取得最大值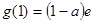


科目:高中数学 来源: 题型:解答题
岛A观察站发现在其东南方向有一艘可疑船只,正以每小时10海里的速度向东南方向航行,观察站即刻通知在岛A正南方向B处巡航的海监船前往检查.接到通知后,海监船测得可疑船只在其北偏东75°方向且相距10海里的C处,随即以每小时10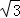 海里的速度前往拦截.
海里的速度前往拦截.
(I)问:海监船接到通知时,距离岛A多少海里?
(II)假设海监船在D处恰好追上可疑船只,求它的航行方向及其航行的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“城中观海”是近年来国内很多大中型城市内涝所致的现象,究其原因,除天气因素、城市规划等原因外,城市垃圾杂物也是造成内涝的一个重要原因。暴雨会冲刷城市的垃圾杂物一起进入下水道,据统计,在不考虑其它因素的条件下,某段下水道的排水量V(单位:立方米/小时)是杂物垃圾密度x(单位:千克/立方米)的函数。当下水道的垃圾杂物密度达到2千克/立方米时,会造成堵塞,此时排水量为0;当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时;研究表明,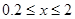 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。
(Ⅰ)当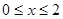 时,求函数V(x)的表达式;
时,求函数V(x)的表达式;
(Ⅱ)当垃圾杂物密度x为多大时,垃圾杂物量(单位时间内通过某段下水道的垃圾杂物量,单位:千克/小时) 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com