
设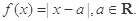
(Ⅰ)当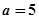 ,解不等式
,解不等式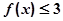 ;
;
(Ⅱ)当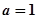 时,若
时,若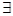
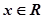 ,使得不等式
,使得不等式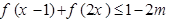 成立,求实数
成立,求实数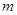 的取值范围.
的取值范围.
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数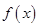 的自变量的取值区间为A,若其值域区间也为A,则称A为
的自变量的取值区间为A,若其值域区间也为A,则称A为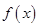 的保值区间.
的保值区间.
(Ⅰ)求函数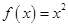 形如
形如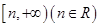 的保值区间;
的保值区间;
(Ⅱ)函数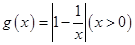 是否存在形如
是否存在形如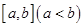 的保值区间?若存在,求出实数
的保值区间?若存在,求出实数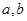 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某厂家准备在2013年12月份举行促销活动,依以往的数据分析,经测算,该产品的年销售量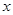 万件(假设该厂生产的产品全部销售),与年促销费用
万件(假设该厂生产的产品全部销售),与年促销费用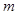 万元
万元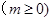 近似满足
近似满足 ,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).
,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).
(1)将2013年该产品的年利润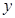 万元表示为年促销费用
万元表示为年促销费用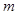 万元的函数;
万元的函数;
(2)该厂家2013年的年促销费用投入为多少万元时,该厂家的年利润最大?并求出年最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某林场现有木材30000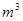 ,如果每年平均增长5﹪,经过
,如果每年平均增长5﹪,经过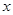 年,树林中有木材
年,树林中有木材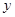
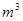 ,
,
(1)写出木材储量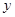 (
(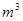 )与
)与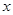 之间的函数关系式。
之间的函数关系式。
(2)经过多少年储量不少于60000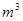 ?(结果保留一个有效数字)
?(结果保留一个有效数字)
(参考数据: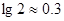 ,
,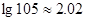 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
湖北省第十四届运动会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向荆州筹委会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为 元,
元, 为整数.
为整数.
(1)写出该专营店一年内销售这种纪念章所获利润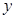 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格 (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每枚纪念章销售价格 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润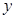 (元)最大,并求出最大值.
(元)最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一种放射性元素,最初的质量为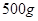 ,按每年
,按每年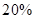 衰减.
衰减.
(1)求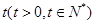 年后,这种放射性元素的质量
年后,这种放射性元素的质量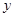 与
与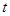 的函数关系式;
的函数关系式;
(2)求这种放射性元素的半衰期(质量变为原来的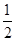 时所经历的时间).(
时所经历的时间).(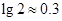 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
集合A是由适合以下性质的函数 构成的:对于定义域内任意两个不相等的实数
构成的:对于定义域内任意两个不相等的实数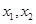 ,都有
,都有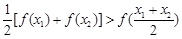 .
.
(1)试判断 =
=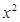 及
及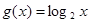 是否在集合A中,并说明理由;
是否在集合A中,并说明理由;
(2)设 ÎA且定义域为(0,+¥),值域为(0,1),
ÎA且定义域为(0,+¥),值域为(0,1), ,试写出一个满足以上条件的函数
,试写出一个满足以上条件的函数 的解析式,并给予证明.
的解析式,并给予证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com