
已知二次函数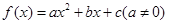 的图像顶点为
的图像顶点为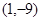 ,且图像在
,且图像在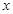 轴截得的线段长为6.
轴截得的线段长为6.
(Ⅰ)求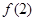 ;
;
(Ⅱ)若 在区间
在区间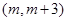 上单调,求
上单调,求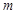 的范围.
的范围.
科目:高中数学 来源: 题型:解答题
己知函数f(x)=ex,x R.
R.
(1)若直线y=kx+1与f(x)的反函数图象相切,求实数k的值;
(2)设x﹥0,讨论曲线y=f(x)与曲线y=mx2(m﹥0)公共点的个数;
(3)设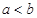 ,比较
,比较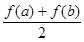 与
与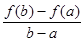 的大小并说明理由。
的大小并说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
为了在夏季降温和冬季供暖时减少能源消耗,房屋的屋顶和外墙需要建造隔热层,某栋建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度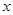 (单位:
(单位: )满足关系:
)满足关系:
若不建隔热层,每年能源消耗费用为8万元。设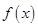 为隔热层建造费用与20年的能源消耗费用之和。
为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求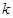 的值及
的值及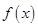 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用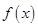 最小,并求最小值.
最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某产品生产厂家根据以往的生产销售经验得到下面有关生产销售的统计规律:每生产产品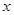 (百台),其总成本为
(百台),其总成本为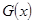 (万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入
(万元),其中固定成本为2.8万元,并且每生产1百台的生产成本为1万元(总成本=固定成本+生产成本)。销售收入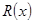 (万元)满足
(万元)满足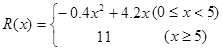 ,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
,假定该产品产销平衡(即生产的产品都能卖掉),根据上述统计规律,请完成下列问题:
分别写出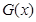 和利润函数
和利润函数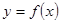 的解析式(利润=销售收入—总成本);
的解析式(利润=销售收入—总成本);
工厂生产多少台产品时,可使盈利最多?并求出此时每台产品的售价。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com