
湖北省第十四届运动会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向荆州筹委会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为 元,
元, 为整数.
为整数.
(1)写出该专营店一年内销售这种纪念章所获利润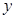 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格 (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每枚纪念章销售价格 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润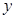 (元)最大,并求出最大值.
(元)最大,并求出最大值.
(1)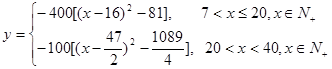 ,定义域为
,定义域为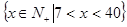
(2)当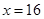 时,该特许专营店获得的利润最大为32400元.
时,该特许专营店获得的利润最大为32400元.
解析试题分析:此题主要考查学生对函数模型在实际问题中应用的能力.(1)在此类问题中要注意单价与销售量之间的相关关系,同时要注意单价价格的取值范围,必要时要进行分段列式,再根据题意求解;(2)经审题实际问题是求函数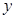 的最大值,由(1)可知函数
的最大值,由(1)可知函数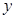 是分段函数,所以要在自变量的各区间中求出最大值,进行比较,从而求出函数的最大值,再还原回实际问题的解.
是分段函数,所以要在自变量的各区间中求出最大值,进行比较,从而求出函数的最大值,再还原回实际问题的解.
试题解析:(1)依题意
∴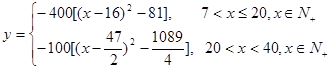 ,
,
定义域为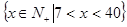 6分
6分
(2)∵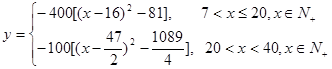 ,]
,]
∴ 当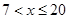 时,则
时,则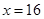 ,
,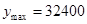 (元)
(元)
当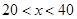 时,则
时,则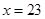 或24,
或24,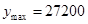 (元)
(元)
综上:当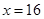 时,该特许专营店获得的利润最大为32400元. 13分
时,该特许专营店获得的利润最大为32400元. 13分
考点:1.实际问题中的函数建模;2.分段函数的最值;3.二次函数的最值.


科目:高中数学 来源: 题型:解答题
为了降低能源损耗,某体育馆的外墙需要建造隔热层.体育馆要建造可使用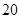 年的隔热层,每厘米厚的隔热层建造成本为
年的隔热层,每厘米厚的隔热层建造成本为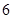 万元.该建筑物每年的能源消耗费用
万元.该建筑物每年的能源消耗费用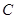 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度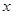 (单位:
(单位: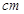 )满足关系:
)满足关系: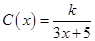 (
(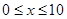 ,
, 为常数),若不建隔热层,每年能源消耗费用为
为常数),若不建隔热层,每年能源消耗费用为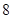 万元.设
万元.设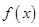 为隔热层建造费用与
为隔热层建造费用与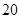 年的能源消耗费用之和.
年的能源消耗费用之和.
(1)求 的值及
的值及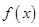 的表达式;
的表达式;
(2)隔热层修建多厚时,总费用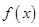 达到最小,并求最小值.
达到最小,并求最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示, 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园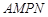 ,要求:B在
,要求:B在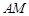 上,D在
上,D在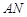 上,对角线
上,对角线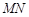 过C点,且矩形
过C点,且矩形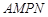 的面积小于64平方米.
的面积小于64平方米.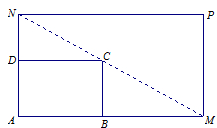
(Ⅰ)设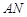 长为
长为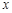 米,矩形
米,矩形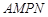 的面积为
的面积为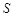 平方米,试用解析式将
平方米,试用解析式将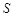 表示成
表示成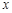 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(Ⅱ)当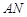 的长度是多少时,矩形
的长度是多少时,矩形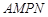 的面积最小?并求最小面积.
的面积最小?并求最小面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com