
已知函数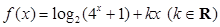 是偶函数。
是偶函数。
(1)求 的值;
的值;
(2)设函数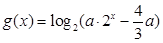 ,其中实数
,其中实数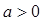 。若函数
。若函数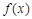 与
与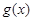 的图象有且只有一个交点,求实数
的图象有且只有一个交点,求实数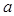 的取值范围。
的取值范围。
(1)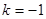 ;(2)
;(2)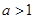
解析试题分析:(1)根据偶函数定义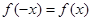 可得到关于k的方程,根据对应系数相等可解出k的值。(2)由题意分析可知将函数
可得到关于k的方程,根据对应系数相等可解出k的值。(2)由题意分析可知将函数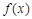 与
与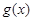 的图象有且只有一个交点的问题 为方程
的图象有且只有一个交点的问题 为方程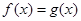 只有一个根的问题。将
只有一个根的问题。将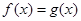 整理变形并结合换元法可转化为
整理变形并结合换元法可转化为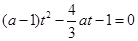 ,在
,在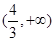 上只有一个解的问题。因为此二次函数对称轴是变量,属于动轴定区间问题。分情况讨论,详见解析。
上只有一个解的问题。因为此二次函数对称轴是变量,属于动轴定区间问题。分情况讨论,详见解析。
试题解析:解:(1)∵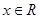 由题有
由题有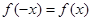 对
对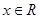 恒成立 …2分
恒成立 …2分
即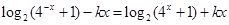 恒成立,整理得
恒成立,整理得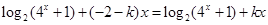 ,所以
,所以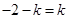 ∴
∴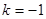
(2)由函数的定义域得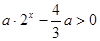 , 由于
, 由于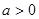
所以 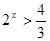 即定义域为
即定义域为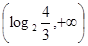
∵函数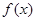 与
与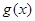 的图象有且只有一个交点,即方程
的图象有且只有一个交点,即方程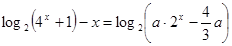 在
在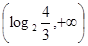 上只有一解。
上只有一解。
即:方程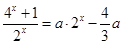 在
在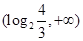 上只有一解
上只有一解
令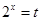 ,则
,则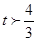 ,上式可变形为
,上式可变形为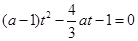 ,在
,在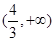 上只有一个解。
上只有一个解。
当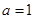 时,
时, 舍。
舍。
当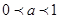 时,记
时,记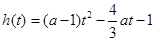 ,其图像的对称轴为
,其图像的对称轴为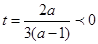 ,所以
,所以 在
在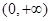 上单调递减,而
上单调递减,而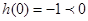 。所以方程
。所以方程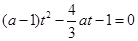 在
在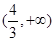 上无解。
上无解。
当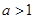 时,记
时,记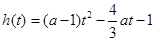 ,其图象的对称轴
,其图象的对称轴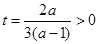
所以只需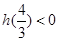 ,即
,即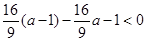 ,此恒成立
,此恒成立
∴此时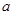 的范围为
的范围为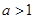
综上所述,所求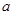 的取值范围为
的取值范围为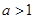
考点:奇偶性,数形结合思想,二次函数的动轴定区间问题


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)= ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).
(1)求h(a);
(2)是否存在实数m、n同时满足下列条件:
①m>n>3;
②当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m、n的值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某单位拟建一个扇环面形状的花坛(如图所示),该扇环面是由以点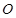 为圆心的两个同心圆弧和延长后通过点
为圆心的两个同心圆弧和延长后通过点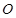 的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为
的两条直线段围成.按设计要求扇环面的周长为30米,其中大圆弧所在圆的半径为10米.设小圆弧所在圆的半径为 米,圆心角为
米,圆心角为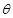 (弧度).
(弧度).
(1)求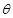 关于
关于 的函数关系式;
的函数关系式;
(2)已知在花坛的边缘(实线部分)进行装饰时,直线部分的装饰费用为4元/米,弧线部分的装饰费用为9元/米.设花坛的面积与装饰总费用的比为 ,求
,求 关于
关于 的函数关系式,并求出
的函数关系式,并求出 为何值时,
为何值时, 取得最大值?
取得最大值?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是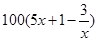 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数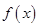 的自变量的取值区间为A,若其值域区间也为A,则称A为
的自变量的取值区间为A,若其值域区间也为A,则称A为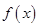 的保值区间.
的保值区间.
(Ⅰ)求函数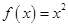 形如
形如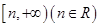 的保值区间;
的保值区间;
(Ⅱ)函数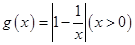 是否存在形如
是否存在形如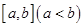 的保值区间?若存在,求出实数
的保值区间?若存在,求出实数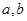 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
湖北省第十四届运动会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向荆州筹委会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为 元,
元, 为整数.
为整数.
(1)写出该专营店一年内销售这种纪念章所获利润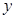 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格 (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每枚纪念章销售价格 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润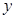 (元)最大,并求出最大值.
(元)最大,并求出最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com