
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是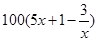 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
(1)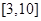 ;(2)以每小时6千克的速度能获得最大利润,最大利润为457500元.
;(2)以每小时6千克的速度能获得最大利润,最大利润为457500元.
解析试题分析:(1)函数应用题是高考的常考内容,一般都是根据题意列出函数式,不等式,方程,而其关系式大多在题目里都有提示,我们只要按照题意列出相应式子,然后根据对应的知识解题即可,如本题就是列出不等式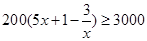 ,这个不等式的解就是所求范围.(2)求利润最大问题,一般是列出函数式,再借助函数的知识解决,本题就是把利润
,这个不等式的解就是所求范围.(2)求利润最大问题,一般是列出函数式,再借助函数的知识解决,本题就是把利润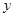 表示为生产速度
表示为生产速度 的函数
的函数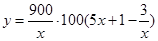 ,这个函数可以看作为关于
,这个函数可以看作为关于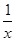 的二次函数,从而可以利用二次函数的知识得解.
的二次函数,从而可以利用二次函数的知识得解.
试题解析:(1)根据题意,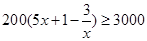
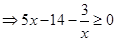 4分
4分
又 ,可解得
,可解得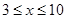 6分
6分
因此,所求 的取值范围是
的取值范围是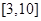 7分
7分
(2)设利润为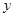 元,则
元,则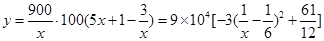 11分
11分
故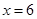 时,
时,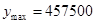 元. 13分
元. 13分
因此该工厂应该以每小时6千克的速度生产才能获得最大利润,最大利润为457500元. 14分
14分
考点:(1)列解不等式;(2)函数的最值.


科目:高中数学 来源: 题型:解答题
已知函数f(x)= 的图象过原点,且关于点(-1,2)成中心对称.
的图象过原点,且关于点(-1,2)成中心对称.
(1)求函数f(x)的解析式;
(2)若数列{an}满足a1=2,an+1=f(an),试证明数列 为等比数列,并求出数列{an}的通项公式.
为等比数列,并求出数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价 元与日销售量
元与日销售量 件之间有如下关系:
件之间有如下关系:
| x | 45 | 50 |
| y | 27 | 12 |
 与
与 的一个一次函数关系式
的一个一次函数关系式 ;
; 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某地方政府准备在一块面积足够大的荒地上建一如图所示的一个矩形综合性休闲广场,其总面积为3000平方米,其中场地四周(阴影部分)为通道,通道宽度均为2米,中间的三个矩形区域将铺设塑胶地面作为运动场地(其中两个小场地形状相同),塑胶运动场地占地面积为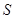 平方米.
平方米.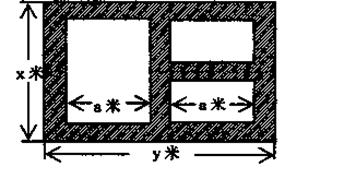
(1)分别写出用 表示
表示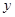 和用
和用 表示
表示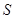 的函数关系式(写出函数定义域);
的函数关系式(写出函数定义域);
(2)怎样设计能使S取得最大值,最大值为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种海洋生物身体的长度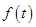 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: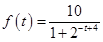 .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)该生物出生后第3年和第4年各长了多少米?并据此判断,这2年中哪一年长得更快.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 ,h(x)=2alnx,
,h(x)=2alnx,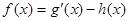 .
.
(1)当a∈R时,讨论函数 的单调性;
的单调性;
(2)是否存在实数a,对任意的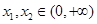 ,且
,且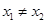 ,都有
,都有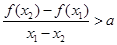
恒成立,若存在,求出a的取值范围;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示, 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园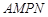 ,要求:B在
,要求:B在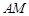 上,D在
上,D在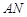 上,对角线
上,对角线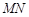 过C点,且矩形
过C点,且矩形 的面积小于64平方米.
的面积小于64平方米.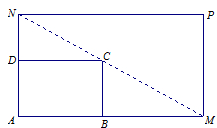
(Ⅰ)设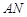 长为
长为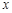 米,矩形
米,矩形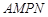 的面积为
的面积为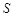 平方米,试用解析式将
平方米,试用解析式将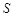 表示成
表示成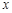 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(Ⅱ)当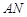 的长度是多少时,矩形
的长度是多少时,矩形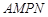 的面积最小?并求最小面积.
的面积最小?并求最小面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com