
已知函数 ,h(x)=2alnx,
,h(x)=2alnx,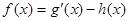 .
.
(1)当a∈R时,讨论函数 的单调性;
的单调性;
(2)是否存在实数a,对任意的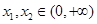 ,且
,且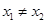 ,都有
,都有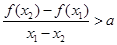
恒成立,若存在,求出a的取值范围;若不存在,说明理由.
(1)详见解析;(2)不存在.
解析试题分析:(1)讨论函数的单调性,在定义域内研究其导函数的符号即可.先求导函数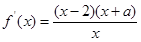
,因为定义域为 ,故只需讨论分子符号,可结合二次函数的图象判断,此时①需讨论交点
,故只需讨论分子符号,可结合二次函数的图象判断,此时①需讨论交点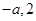 的大小,②注意根与定义域比较,所以
的大小,②注意根与定义域比较,所以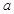 需和-2和0比较大小;(2)由对称性,不妨设
需和-2和0比较大小;(2)由对称性,不妨设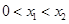 ,去分母得
,去分母得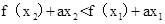 ,构造函数
,构造函数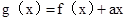 ,则其在定义域内单调递减,故
,则其在定义域内单调递减,故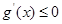 在
在 恒成立,而
恒成立,而 ,分子二次函数开口向上,不可能永远小于0,故不存在.
,分子二次函数开口向上,不可能永远小于0,故不存在.
试题解析:(1)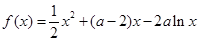 ,∴
,∴ 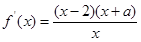 ,
,  的定义域为
的定义域为 .
.
①当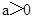 时,
时, 在
在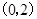 上是减函数,在在
上是减函数,在在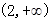 上是增函数;
上是增函数;
②当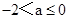 时,
时, 在
在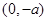 上是增函数;在
上是增函数;在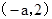 是是减函数;在
是是减函数;在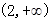 上是增函数;
上是增函数;
③当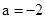 时,
时, 在
在 上是增函数;
上是增函数;
④当 时,
时, 在
在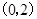 上是增函数;在
上是增函数;在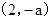 上是减函数;在
上是减函数;在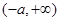 上是增函数.
上是增函数.
(2)假设存在实数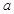 ,对任意的
,对任意的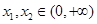 ,且
,且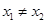 ,都有
,都有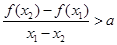 恒成立,不妨设
恒成立,不妨设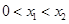 ,要使
,要使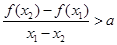 ,即
,即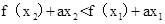 .
.
令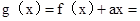
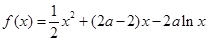 ,只要
,只要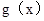 在
在 为减函数.
为减函数.
又 ,由题意
,由题意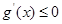 在
在 上恒成立,得
上恒成立,得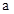 不存在.
不存在.
考点:1、导数在单调性上的应用;2、二次函数的图象;3、函数思想的应用.


科目:高中数学 来源: 题型:解答题
若函数f(x)对任意的实数x1,x2∈D,均有|f(x2)-f(x1)|≤|x2-x1|,则称函数f(x)是区间D上的“平缓函数”.
(1)判断g(x)=sin x和h(x)=x2-x是不是实数集R上的“平缓函数”,并说明理由;
(2)若数列{xn}对所有的正整数n都有|xn+1-xn|≤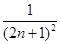 ,设yn=sin xn,求证:|yn+1-y1|<
,设yn=sin xn,求证:|yn+1-y1|< .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是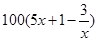 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com