
如图所示, 是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛
是一个矩形花坛,其中AB=4米,AD=3米.现将矩形花坛 扩建成一个更大的矩形花园
扩建成一个更大的矩形花园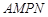 ,要求:B在
,要求:B在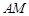 上,D在
上,D在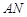 上,对角线
上,对角线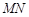 过C点,且矩形
过C点,且矩形 的面积小于64平方米.
的面积小于64平方米.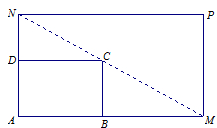
(Ⅰ)设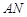 长为
长为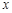 米,矩形
米,矩形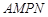 的面积为
的面积为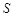 平方米,试用解析式将
平方米,试用解析式将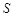 表示成
表示成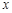 的函数,并写出该函数的定义域;
的函数,并写出该函数的定义域;
(Ⅱ)当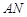 的长度是多少时,矩形
的长度是多少时,矩形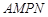 的面积最小?并求最小面积.
的面积最小?并求最小面积.
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:解答题
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是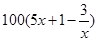 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某林场现有木材30000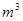 ,如果每年平均增长5﹪,经过
,如果每年平均增长5﹪,经过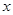 年,树林中有木材
年,树林中有木材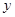
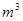 ,
,
(1)写出木材储量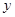 (
(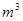 )与
)与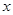 之间的函数关系式。
之间的函数关系式。
(2)经过多少年储量不少于60000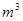 ?(结果保留一个有效数字)
?(结果保留一个有效数字)
(参考数据: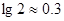 ,
,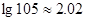 )
)
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂某种产品的年固定成本为250万元,每生产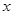 千件,需另投入成本为
千件,需另投入成本为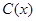 ,当年产量不足80千件时,
,当年产量不足80千件时,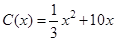 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润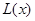 (万元)关于年产量
(万元)关于年产量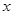 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
湖北省第十四届运动会纪念章委托某专营店销售,每枚进价5元,同时每销售一枚这种纪念章需向荆州筹委会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时该店一年可销售2000枚,经过市场调研发现每枚纪念章的销售价格在每枚20元的基础上每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为 元,
元, 为整数.
为整数.
(1)写出该专营店一年内销售这种纪念章所获利润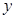 (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格 (元)的函数关系式(并写出这个函数的定义域);
(元)的函数关系式(并写出这个函数的定义域);
(2)当每枚纪念章销售价格 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润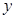 (元)最大,并求出最大值.
(元)最大,并求出最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
用一块钢锭烧铸一个厚度均匀,且表面积为2m2的正四棱锥形有盖容器(如下图)。设容器高为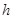 m,盖子边长为
m,盖子边长为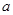 m,
m,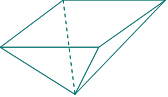
(1)求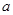 关于
关于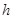 的解析式;
的解析式;
(2)设容器的容积为V m3,则当h为何值时,V最大? 并求出V的最大值(求解本题时,不计容器厚度).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com