
某种海洋生物身体的长度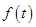 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: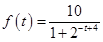 .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)该生物出生后第3年和第4年各长了多少米?并据此判断,这2年中哪一年长得更快.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
经市场调查,某旅游城市在过去的一个月内(以30天计),旅游人数f(t)(万人)与时间t(天)的函数关系近似满足f(t)=4+ ,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|.
,人均消费g(t)(元)与时间t(天)的函数关系近似满足g(t)=115-|t-15|.
(1)求该城市的旅游日收益w(t)(万元)与时间t(1≤t≤30,t∈N*)的函数关系式;
(2)求该城市旅游日收益的最小值(万元).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
心理学家通过研究学生的学习行为发现;学生的接受能力与老师引入概念和描述问题所用的时间相关,教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用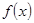 表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系: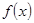
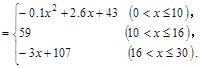
(1)开讲后第5min与开讲后第20min比较,学生的接受能力何时更强一些?
(2)开讲后多少min学生的接受能力最强?能维持多少时间?
(3)若一个新数学概念需要55以上(包括55)的接受能力以及13min时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
噪声污染已经成为影响人们身体健康和生活质量的严重问题.实践证明,声音强度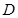 (分贝)由公式
(分贝)由公式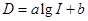 (
(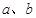 为非零常数)给出,其中
为非零常数)给出,其中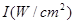 为声音能量.
为声音能量.
(1)当声音强度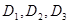 满足
满足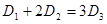 时,求对应的声音能量
时,求对应的声音能量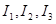 满足的等量关系式;
满足的等量关系式;
(2)当人们低声说话,声音能量为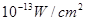 时,声音强度为30分贝;当人们正常说话,声音能量为
时,声音强度为30分贝;当人们正常说话,声音能量为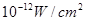 时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
时,声音强度为40分贝.当声音能量大于60分贝时属于噪音,一般人在100分贝~120分贝的空间内,一分钟就会暂时性失聪.问声音能量在什么范围时,人会暂时性失聪.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
上海某化学试剂厂以x千克/小时的速度生产某种产品(生产条件要求 ),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是
),为了保证产品的质量,需要一边生产一边运输,这样按照目前的市场价格,每小时可获得利润是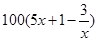 元.
元.
(1)要使生产运输该产品2小时获得的利润不低于3000元,求x的取值范围;
(2)要使生产运输900千克该产品获得的利润最大,问:该工厂应该选取何种生产速度?并求最大利润.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“地沟油”严重危害了人民群众的身体健康,某企业在政府部门的支持下,进行技术攻关,新上了一种从“食品残渣”中提炼出生物柴油的项目,经测算,该项目月处理成本y(元)与月处理量x(吨)之间的函数关系可以近似的表示为: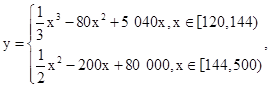
且每处理一吨“食品残渣”,可得到能利用的生物柴油价值为200元,若该项目不获利,政府将补贴.
(1)当x∈[200,300]时,判断该项目能否获利?如果获利,求出最大利润;如果不获利,则政府每月至少需要补贴多少元才能使该项目不亏损;
(2)该项目每月处理量为多少吨时,才能使每吨的平均处理成本最低?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂某种产品的年固定成本为250万元,每生产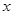 千件,需另投入成本为
千件,需另投入成本为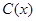 ,当年产量不足80千件时,
,当年产量不足80千件时,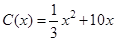 (万元).当年产量不小于80千件时,
(万元).当年产量不小于80千件时, (万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为500元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润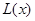 (万元)关于年产量
(万元)关于年产量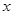 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com