
心理学家通过研究学生的学习行为发现;学生的接受能力与老师引入概念和描述问题所用的时间相关,教学开始时,学生的兴趣激增,学生的兴趣保持一段较理想的状态,随后学生的注意力开始分散,分析结果和实验表明,用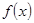 表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系:
表示学生掌握和接受概念的能力, x表示讲授概念的时间(单位:min),可有以下的关系: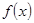
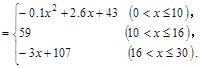
(1)开讲后第5min与开讲后第20min比较,学生的接受能力何时更强一些?
(2)开讲后多少min学生的接受能力最强?能维持多少时间?
(3)若一个新数学概念需要55以上(包括55)的接受能力以及13min时间,那么老师能否在学生一直达到所需接受能力的状态下讲授完这个概念?
(1)开讲后第5min比开讲后第20min,学生接受能力强一些.;(2)6min; (3)详见解析.
解析试题分析:此题考查的是分段函数的基本知识及分段函数图象增减性的应用.第一小题求学生的接受能力最强其实就是要求分段函数的最大值,方法是分别求出各段的最大值取其最大即可.第二小题比较5分钟和15分钟学生的接受能力何时强,方法是把x=5代入第一段函数中,而x=15要代入到第二段函数中,比较大小即可.不同的自变量代入相应的解析式才能符合要求.第三小题考查分段函数图象和增减性,令f(x)=55,第一段函数解得x=6,第二段函数解得x=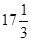 ,关键是从图象上知道6<x<
,关键是从图象上知道6<x<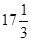
时,f(x)>55,然后求出两个时间之差即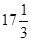 -6=
-6=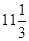 ,其实就是持续的时间,最后和10分钟比较大小即可.
,其实就是持续的时间,最后和10分钟比较大小即可.
试题解析::(1) 2分
2分 开讲后第5min比开讲后第20min,学生接受能力强一些. 3分
开讲后第5min比开讲后第20min,学生接受能力强一些. 3分
(2)当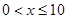 时,
时,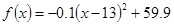 4分
4分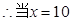 时
时 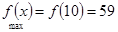 5分
5分
当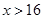 时,
时,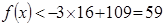 6分
6分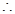 开讲后10mim(包括10mim)学生接受能力最强,能维持6min.7分
开讲后10mim(包括10mim)学生接受能力最强,能维持6min.7分
(3)由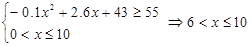 9分
9分
又由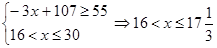 , 11分
, 11分
故接受概念的能力在55以上(包括55)的时间为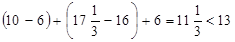
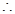 老师不能在学生一直达到所需接受能力的的状态下讲授完这个新概念12分
老师不能在学生一直达到所需接受能力的的状态下讲授完这个新概念12分
考点:根据实际问题选择函数类型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
现有A,B两个投资项目,投资两项目所获得利润分别是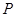 和
和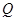 (万元),它们与投入资金
(万元),它们与投入资金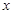 (万元)的关系依次是:其中
(万元)的关系依次是:其中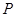 与
与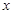 平方根成正比,且当
平方根成正比,且当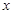 为4(万元)时
为4(万元)时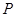 为1(万元),又
为1(万元),又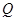 与
与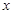 成正比,当
成正比,当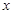 为4(万元)时
为4(万元)时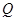 也是1(万元);某人甲有3万元资金投资.
也是1(万元);某人甲有3万元资金投资.
(1)分别求出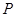 ,
,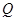 与
与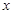 的函数关系式;
的函数关系式;
(2)请帮甲设计一个合理的投资方案,使其获利最大,并求出最大利润是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
我国西部某省4A级风景区内住着一个少数民族村,该村投资了800万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按30天计算)每天的旅游人数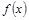 与第x天近似地满足
与第x天近似地满足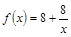 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费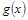 近似地满足
近似地满足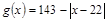 (元).
(元).
(1)求该村的第x天的旅游收入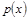 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,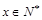 )的函数关系;
)的函数关系;
(2)若以最低日收入的20%作为每一天的计量依据,并以纯收入的5%的税率收回投资成本,试问该村在两年内能否收回全部投资成本?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场经营一批进价是30元/件的商品,在市场试销中发现,此商品销售价 元与日销售量
元与日销售量 件之间有如下关系:
件之间有如下关系:
| x | 45 | 50 |
| y | 27 | 12 |
 与
与 的一个一次函数关系式
的一个一次函数关系式 ;
; 的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?
的函数关系,并指出当销售单价为多少元时,才能获得最大的日销售利润?查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某种海洋生物身体的长度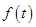 (单位:米)与生长年限t(单位:年)
(单位:米)与生长年限t(单位:年)
满足如下的函数关系: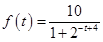 .(设该生物出生时t=0)
.(设该生物出生时t=0)
(1)需经过多少时间,该生物的身长超过8米;
(2)该生物出生后第3年和第4年各长了多少米?并据此判断,这2年中哪一年长得更快.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在一条笔直的工艺流水线上有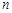 个工作台,将工艺流水线用如图
个工作台,将工艺流水线用如图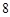 所示的数轴表示,各工作台的坐标分别为
所示的数轴表示,各工作台的坐标分别为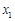 ,
,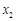 ,
,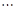 ,
,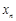 ,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.
,每个工作台上有若干名工人.现要在流水线上建一个零件供应站,使得各工作台上的所有工人到供应站的距离之和最短.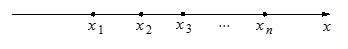
(Ⅰ)若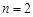 ,每个工作台上只有一名工人,试确定供应站的位置;
,每个工作台上只有一名工人,试确定供应站的位置;
(Ⅱ)若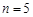 ,工作台从左到右的人数依次为
,工作台从左到右的人数依次为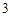 ,
,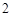 ,
,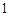 ,
,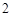 ,
,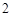 ,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
,试确定供应站的位置,并求所有工人到供应站的距离之和的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com