
集合A是由适合以下性质的函数 构成的:对于定义域内任意两个不相等的实数
构成的:对于定义域内任意两个不相等的实数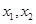 ,都有
,都有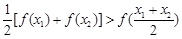 .
.
(1)试判断 =
=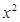 及
及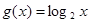 是否在集合A中,并说明理由;
是否在集合A中,并说明理由;
(2)设 ÎA且定义域为(0,+¥),值域为(0,1),
ÎA且定义域为(0,+¥),值域为(0,1), ,试写出一个满足以上条件的函数
,试写出一个满足以上条件的函数 的解析式,并给予证明.
的解析式,并给予证明.
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案科目:高中数学 来源: 题型:解答题
岛A观察站发现在其东南方向有一艘可疑船只,正以每小时10海里的速度向东南方向航行,观察站即刻通知在岛A正南方向B处巡航的海监船前往检查.接到通知后,海监船测得可疑船只在其北偏东75°方向且相距10海里的C处,随即以每小时10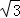 海里的速度前往拦截.
海里的速度前往拦截.
(I)问:海监船接到通知时,距离岛A多少海里?
(II)假设海监船在D处恰好追上可疑船只,求它的航行方向及其航行的时间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
对于函数 若存在
若存在 ,使得
,使得 成立,则称
成立,则称 为
为 的不动点.
的不动点.
已知
(1)当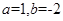 时,求函数
时,求函数 的不动点;
的不动点;
(2)若对任意实数 ,函数
,函数 恒有两个相异的不动点,求
恒有两个相异的不动点,求 的取值范围;
的取值范围;
(3)在(2)的条件下,若 图象上
图象上 、
、 两点的横坐标是函数
两点的横坐标是函数 的不动点,且
的不动点,且 、
、 两点关于直线
两点关于直线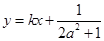 对称,求
对称,求 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
“城中观海”是近年来国内很多大中型城市内涝所致的现象,究其原因,除天气因素、城市规划等原因外,城市垃圾杂物也是造成内涝的一个重要原因。暴雨会冲刷城市的垃圾杂物一起进入下水道,据统计,在不考虑其它因素的条件下,某段下水道的排水量V(单位:立方米/小时)是杂物垃圾密度x(单位:千克/立方米)的函数。当下水道的垃圾杂物密度达到2千克/立方米时,会造成堵塞,此时排水量为0;当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时;研究表明,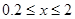 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。
(Ⅰ)当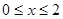 时,求函数V(x)的表达式;
时,求函数V(x)的表达式;
(Ⅱ)当垃圾杂物密度x为多大时,垃圾杂物量(单位时间内通过某段下水道的垃圾杂物量,单位:千克/小时) 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某工厂有 名工人,现接受了生产
名工人,现接受了生产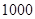 台
台 型高科技产品的总任务.已知每台
型高科技产品的总任务.已知每台 型产品由
型产品由 个
个 型装置和
型装置和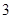 个
个 型装置配套组成,每个工人每小时能加工
型装置配套组成,每个工人每小时能加工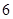 个
个 型装置或
型装置或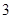 个
个 型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工
型装置.现将工人分成两组同时开始加工,每组分别加工一种装置(完成自己的任务后不再支援另一组).设加工 型装置的工人有
型装置的工人有 人,他们加工完
人,他们加工完 型装置所需时间为
型装置所需时间为 ,其余工人加工完
,其余工人加工完 型装置所需时间为
型装置所需时间为 (单位:小时,可不为整数).
(单位:小时,可不为整数).
(1)写出 、
、 的解析式;
的解析式;
(2)写出这 名工人完成总任务的时间
名工人完成总任务的时间 的解析式;
的解析式;
(3)应怎样分组,才能使完成总任务用的时间最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com