
已知某公司生产品牌服装的年固定成本为10万元,每生产千件,须另投入2.7万元,设该公司年内共生产品牌服装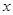 千件并全部销售完,每千件的销售收入为
千件并全部销售完,每千件的销售收入为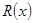 万元,且
万元,且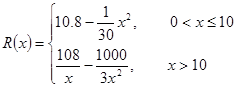 .
.
(1)写出年利润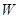 (万元)关于年产量
(万元)关于年产量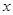 (千件)的函数解析式;
(千件)的函数解析式;
(2)当年产量为多少千件时,该公司在这一品牌服装的生产中所获年利润最大?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
“城中观海”是近年来国内很多大中型城市内涝所致的现象,究其原因,除天气因素、城市规划等原因外,城市垃圾杂物也是造成内涝的一个重要原因。暴雨会冲刷城市的垃圾杂物一起进入下水道,据统计,在不考虑其它因素的条件下,某段下水道的排水量V(单位:立方米/小时)是杂物垃圾密度x(单位:千克/立方米)的函数。当下水道的垃圾杂物密度达到2千克/立方米时,会造成堵塞,此时排水量为0;当垃圾杂物密度不超过0.2千克/立方米时,排水量是90立方米/小时;研究表明,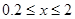 时,排水量V是垃圾杂物密度x的一次函数。
时,排水量V是垃圾杂物密度x的一次函数。
(Ⅰ)当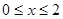 时,求函数V(x)的表达式;
时,求函数V(x)的表达式;
(Ⅱ)当垃圾杂物密度x为多大时,垃圾杂物量(单位时间内通过某段下水道的垃圾杂物量,单位:千克/小时) 可以达到最大,求出这个最大值。
可以达到最大,求出这个最大值。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 的图像与函数h(x)=x++2的图像关于点A(0,1)对称.
的图像与函数h(x)=x++2的图像关于点A(0,1)对称.
(1) 求 的解析式;
的解析式;
(2) 若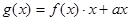 ,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
,且g(x)在区间[0,2]上为减函数,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com