
已知一企业生产某产品的年固定成本为10万元,每生产千件需另投入2.7万元,设该企业年内共生产此种产品 千件,并且全部销售完,每千件的销售收入为
千件,并且全部销售完,每千件的销售收入为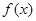 万元,且
万元,且
(1)写出年利润 (万元)关于年产品
(万元)关于年产品 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该企业生产此产品所获年利润最大?
(注:年利润=年销售收入-年总成本)
科目:高中数学 来源: 题型:解答题
已知函数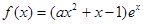 ,其中
,其中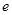 是自然对数的底数,
是自然对数的底数,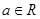 .
.
(1)若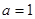 ,求曲线
,求曲线 在点
在点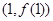 处的切线方程;
处的切线方程;
(2)若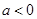 ,求
,求 的单调区间;
的单调区间;
(3)若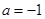 ,函数
,函数 的图象与函数
的图象与函数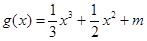 的图象有3个不同的交点,求实数
的图象有3个不同的交点,求实数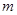 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某商场在店庆一周年开展“购物折上折活动”:商场内所有商品按标价的八折出售,折后价格每满500元再减100元.如某商品标价为1500元,则购买该商品的实际付款额为1500×0.8-200=1000(元).设购买某商品得到的实际折扣率 .设某商品标价为
.设某商品标价为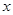 元,购买该商品得到的实际折扣率为
元,购买该商品得到的实际折扣率为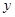 .
.
(Ⅰ)写出当 时,
时,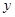 关于
关于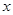 的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
的函数解析式,并求出购买标价为1000元商品得到的实际折扣率;
(Ⅱ)对于标价在[2500,3500]的商品,顾客购买标价为多少元的商品,可得到的实际折扣率低于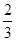 ?
?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com