
分析 (1)函数y=f(x)在其定义域内是单调增函数只需要2ax2+x-1≤0对任意的x>0恒成立,通过分离参数,利用二次函数的性质可求得a的取值范围;
(2)根据二次函数的性质证明并判断|x2-x1|的范围即可.
解答 解:(1)f′(x)=$\frac{1}{x}$-2ax-1=-$\frac{2{ax}^{2}+x-1}{x}$(x>0),
若f(x)在定义域上是增函数,
只需要2ax2+x-1≤0,
即2a≤$\frac{1}{{x}^{2}}$-$\frac{1}{x}$=($\frac{1}{x}$-$\frac{1}{2}$)2-$\frac{1}{4}$,
所以a≤-$\frac{1}{8}$.
(2)证明:由(1)令f′(x)=0,
得:2ax2+x-1=0,
∵-$\frac{1}{9}$≤a≤-$\frac{1}{10}$,
∴△=1+8a>0,
∴方程f′(x)=0有两个不等实根x1,x2,
而x1+x2=-$\frac{1}{2a}$,x1•x2=-$\frac{1}{2a}$,
∴|x2-x1|=$\sqrt{{{(x}_{1}{+x}_{2})}^{2}-{{4x}_{1}x}_{2}}$=$\sqrt{\frac{1}{{4a}^{2}}+\frac{2}{a}}$=$\sqrt{{(\frac{1}{2a}+2)}^{2}-4}$,
∵-$\frac{1}{9}$≤a≤-$\frac{1}{10}$,
∴$\frac{3}{2}$≤|x2-x1|≤$\sqrt{5}$.
点评 本题考查了函数的单调性以及函数恒成立问题,考查导数的应用、二次函数的性质,是一道中档题.


科目:高中数学 来源: 题型:解答题
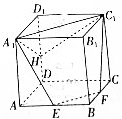 在正方体ABCD-A1B1C1D1中,棱长是1,E,F分别是AB,BC的中点,H是DD1的中点.
在正方体ABCD-A1B1C1D1中,棱长是1,E,F分别是AB,BC的中点,H是DD1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
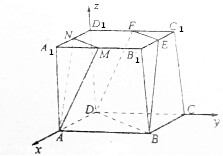 如图,正方体ABCD-A1B1C1D1的棱长为a,点M、N、E、F分别是A1B1、A1D1、B1C1、C1D1的中点,则点M到平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;直线AM与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;平面AMN与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$.
如图,正方体ABCD-A1B1C1D1的棱长为a,点M、N、E、F分别是A1B1、A1D1、B1C1、C1D1的中点,则点M到平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;直线AM与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$;平面AMN与平面EFDB的距离为$\frac{12\sqrt{19}}{19}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 精确值 | B. | 不足近似值 | C. | 过剩近似值 | D. | 以上都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com