
设f(x)= 是奇函数(a>0且a≠1),
是奇函数(a>0且a≠1),
(1)求出m的值
(2)若f(x)的定义域为[α,β](β>α>1),
判断f(x)在定义域上的增减性,并加以证明.
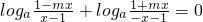
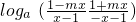 =
=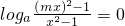
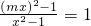 …
…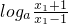
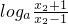 =loga
=loga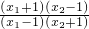
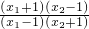 >1
>1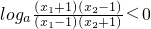 ,即f(x1)<f(x2);
,即f(x1)<f(x2);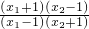 >0,即定义在证明函数f(x1)>f(x2),
>0,即定义在证明函数f(x1)>f(x2),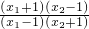 结合已知可判断
结合已知可判断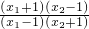 的正负,进而讨论当0<m<1时,及m>1时,f(x1)-f(x2)的符号,即可证明
的正负,进而讨论当0<m<1时,及m>1时,f(x1)-f(x2)的符号,即可证明

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:
| -2x+a | 2x+1+b |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A、设f(x)=sin(2x+
| ||||||
B、?x0∈R.便得
| ||||||
C、设f(x)=cos(x+
| ||||||
D、设f(x)=2sin2x,则f(x+
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com