
【题目】定于符号函数![]() ,已知
,已知![]() ,
,![]() ,
,
(1)求![]() 关于
关于![]() 的表达式,并求
的表达式,并求![]() 的最小值;
的最小值;
(2)当![]() 时,函数
时,函数![]() 在
在![]() 上有唯一零点,求
上有唯一零点,求![]() 的取值范围;
的取值范围;
(3)已知存在![]() ,使得
,使得![]() 对任意
对任意![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据已知求出![]()
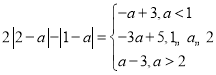 ,分析其单调性可得函数的最小值;
,分析其单调性可得函数的最小值;
(2)当![]() 时,
时,![]() ,由
,由![]() 得:
得:![]() ,即
,即![]() ,令
,令![]() ,
,![]() ,在同一坐标系中分别作出两个函数在
,在同一坐标系中分别作出两个函数在![]() 上的图象,数形结合可得答案;
上的图象,数形结合可得答案;
(3)若存在![]() ,使得
,使得![]() 对任意的
对任意的![]() ,
,![]() 恒成立,则
恒成立,则![]() 对任意的
对任意的![]() ,
,![]() 恒成立,分类讨论可得答案.
恒成立,分类讨论可得答案.
(1)![]() 函数
函数![]() ,
,![]() .
.
![]()
![]() ,
,![]()
![]() ,
,
![]()
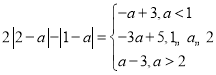 ,
,
由![]() 在
在![]() ,
,![]() 上为减函数,在
上为减函数,在![]() 上为增函数,
上为增函数,
故当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
(2)当![]() 时,函数
时,函数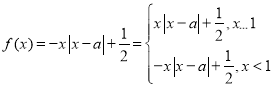 ,
,
当![]() 时,
时,![]() ,
,
由![]() 得:
得:![]() ,即
,即![]() ,
,
令![]() ,
,![]() ,
,
在同一坐标系中分别作出两个函数在![]() 上的图象,如下图所示:
上的图象,如下图所示:
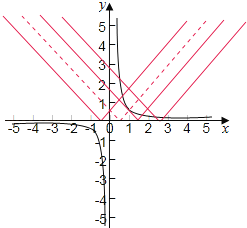
由图可得:当![]() 时,两个函数图象有且只有一个交点,
时,两个函数图象有且只有一个交点,
即函数![]() 在
在![]() 上有唯一零点;
上有唯一零点;
(3)![]() ,
,![]() 时,
时,![]() ,
,
由![]() 得:
得:![]() ,
,
![]() ,且
,且![]() 对任意的
对任意的![]() ,
,![]() 恒成立,
恒成立,
即![]() 对任意的
对任意的![]() ,
,![]() 恒成立,
恒成立,
![]() 在
在![]() ,
,![]() 上单调递增,故当
上单调递增,故当![]() 时,
时,![]() 取最大值
取最大值![]() ,
,
![]() ,
,![]() ,
,![]() 的最小值为
的最小值为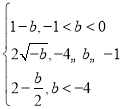 ,
,
①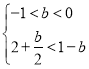 ,解得:
,解得:![]() ;
;
②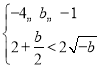 ,解得:
,解得:![]() ,
,![]() ;
;
③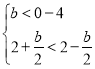 解得:
解得:![]() ,
,
综上可得:![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,正方体![]() 的棱长为
的棱长为![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上的两个动点,且
上的两个动点,且![]() ,则下列结论错误的是 ( )
,则下列结论错误的是 ( )
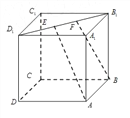
A. ![]()
B. 直线![]() 、
、![]() 所成的角为定值
所成的角为定值
C. ![]() ∥平面
∥平面![]()
D. 三棱锥![]() 的体积为定值
的体积为定值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)从偶函数的定义出发,证明函数![]() 是偶函数的充要条件是它的图象关于y轴对称;
是偶函数的充要条件是它的图象关于y轴对称;
(2)从奇函数的定义出发,证明函数![]() 是奇函数的充要条件是它的图象关于原点对称.
是奇函数的充要条件是它的图象关于原点对称.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有次水下考古活动中,潜水员需潜入水深为30米的水底进行作业,其用氧量包含以下三个方面:①下潜时,平均速度为每分钟![]() 米,每分钟的用氧量为
米,每分钟的用氧量为![]() 升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟
升;②水底作业需要10分钟,每分钟的用氧量为0.3升;③返回水面时,速度为每分钟![]() 米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为
米,每分钟用氧量为0.2升;设潜水员在此次考古活动中的总用氧量为![]() 升;
升;
(1)将![]() 表示为
表示为![]() 的函数;
的函数;
(2)若![]() ,求总用氧量
,求总用氧量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(江苏省南京师大附中2018届高三高考考前模拟考试数学试题)已知函数f(x)=lnx-ax+a,a∈R.
(1)若a=1,求函数f(x)的极值;
(2)若函数f(x)有两个零点,求a的范围;
(3)对于曲线y=f(x)上的两个不同的点P(x1,f(x1)),Q(x2,f(x2)),记直线PQ的斜率为k,若y=f(x)的导函数为f ′(x),证明:f ′(![]() )<k.
)<k.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设P1,P2,…,P6为单位圆上逆时针均匀分布的六个点.现任选其中三个不同点构成一个三角形,记该三角形的面积为随机变量S.
(1)求S=![]() 的概率;
的概率;
(2)求S的分布列及数学期望E(S).

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】空气质量指数AQI是反映空气质量状况的指数,AQI指数值越小,表明空气质量越好,其对应关系如下表:
AQI指数值 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
空气质量 | 优 | 良 | 轻度污染 | 中度污染 | 重度污染 | 严重污染 |
下图是某市10月1日—20日AQI指数变化趋势:

下列叙述错误的是
A. 这20天中AQI指数值的中位数略高于100
B. 这20天中的中度污染及以上的天数占![]()
C. 该市10月的前半个月的空气质量越来越好
D. 总体来说,该市10月上旬的空气质量比中旬的空气质量好
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知函数![]()

(1)若![]() ,用“五点法”在给定的坐标系中,画出函数
,用“五点法”在给定的坐标系中,画出函数![]() 在
在![]() 上的图象.
上的图象.
(2)若![]() 偶函数,求
偶函数,求![]() :
:
(3)在(2)的前提下,将函数![]() 的图象向右平移
的图象向右平移![]() 个单位后,再将得到的图象上各点的横坐标伸长为原来的
个单位后,再将得到的图象上各点的横坐标伸长为原来的![]() 倍,纵坐标不变,再向上平移一个单位得到函数
倍,纵坐标不变,再向上平移一个单位得到函数![]() 的图象,求
的图象,求![]() 的对称中心.
的对称中心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com