练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】如图所示，在正方体ABCDA1B1C1D1中，设线段A1C与平面ABC1D1交于点Q，求证：B，Q，D1三点共线．

    【答案】证明见解析

    【解析】

    如下图所示，连接A1B，CD1．易证BD1平面A1BCD1． BD1平面ABC1D1．即

    平面ABC1D1∩平面A1BCD1＝BD1，下证 Q∈平面A1BCD1．Q∈平面A1BCD1．即可.

    如下图所示，连接A1B，CD1．显然B∈平面A1BCD1，D1∈平面A1BCD1．

    ∴BD1平面A1BCD1．

    同理BD1平面ABC1D1．

    ∴平面ABC1D1∩平面A1BCD1＝BD1．

    ∵A1C∩平面ABC1D1＝Q，

    ∴Q∈平面ABC1D1．

    又∵A1C平面A1BCD1，

    ∴Q∈平面A1BCD1．

    ∴Q∈BD1，即B，Q，D1三点共线．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知抛物线（是正常数）上有两点、，焦点，

    甲：；

    乙：；

    丙：；

    丁：.

    以上是“直线经过焦点”的充要条件有几个（　　）

    A.B.C.D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校有高三文科学生1000人，统计其高三上期期中考试的数学成绩，得到频率分布直方图如下：

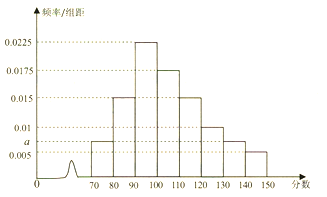
    （1）求出图中的值，并估计本次考试低于120分的人数；

    （2）假设同组的每个数据可用该组区间的中点值代替，试估计本次考试不低于120分的同学的平均数（其结果保留一位小数）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

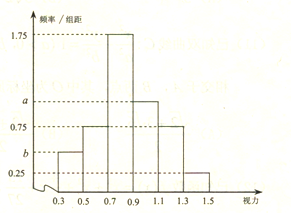
    【题目】从某校高三年级中随机抽取100名学生，对其高校招生体检表中的视图情况进行统计，得到如图所示的频率分布直方图，已知从这100人中随机抽取1人，其视力在的概率为.

    （1）求的值；

    （2）若某大学专业的报考要求之一是视力在0.9以上，则对这100人中能报考专业的学生采用按视力分层抽样的方法抽取8人，调查他们对专业的了解程度，现从这8人中随机抽取3人进行是否有意向报考该大学专业的调查，记抽到的学生中视力在的人数为，求的分布列及数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】给出以下命题：

    ①双曲线的渐近线方程为y＝±x；

    ②命题p：“x∈R，sinx＋≥2”是真命题；

    ③已知线性回归方程为＝3＋2x，当变量x增加2个单位，其预报值平均增加4个单位；

    ④设随机变量ξ服从正态分布N(0,1)，若P(ξ>1)＝0.2，则P(－1<ξ<0)＝0.6；

    ⑤设，则

    则正确命题的序号为________(写出所有正确命题的序号)．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】随着经济模式的改变，微商和电商已成为当今城乡一种新型的购销平台．已知经销某种商品的电商在任何一个销售季度内，没售出1吨该商品可获利润0.5万元，未售出的商品，每1吨亏损0.3万元．根据往年的销售经验，得到一个销售季度内市场需求量的频率分布直方图如图所示．已知电商为下一个销售季度筹备了130吨该商品，现以（单位：吨，）表示下一个销售季度的市场需求量，（单位：万元）表示该电商下一个销售季度内经销该商品获得的利润．

    （Ⅰ）视分布在各区间内的频率为相应的概率，求；

    （Ⅱ）将表示为的函数，求出该函数表达式；

    （Ⅲ）在频率分布直方图的市场需求量分组中，以各组的区间中点值（组中值）代表该组的各个值，并以市场需求量落入该区间的频率作为市场需求量取该组中值的概率（例如，则取的概率等于市场需求量落入的频率），求的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某品牌汽车的店，对最近100份分期付款购车情况进行统计，统计情况如下表所示.已知分9期付款的频率为0.4；该店经销一辆该品牌汽车，若顾客分3期付款，其利润为1万元；分6期或9期付款，其利润为2万元；分12期付款，其利润为3万元.

    付款方式

    分3期

    分6期

    分9期

    分12期

    频数

    20

    20

    （1）若以上表计算出的频率近似替代概率，从该店采用分期付款购车的顾客（数量较大）中随机抽取3为顾客，求事件：“至多有1位采用分6期付款“的概率；

    （2）按分层抽样方式从这100为顾客中抽取5人，再从抽取的5人中随机抽取3人，记该店在这3人身上赚取的总利润为随机变量，求的分布列和数学期望.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知幂函数（）在是单调减函数，且为偶函数.

    （1）求的解析式；

    （2）讨论的奇偶性，并说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设圆的圆心为A，直线过点B（1,0）且与轴不重合，交圆A于C，D两点，过B作AC的平行线交AD于点E.

    （Ⅰ）证明：为定值，并写出点E的轨迹方程；

    （Ⅱ）设点E的轨迹为曲线C1，直线交C1于M,N两点，过B且与垂直的直线与C1交于P,Q两点， 求证：是定值，并求出该定值.

    查看答案和解析>>

    同步练习册答案