
若存在实常数 和
和 ,使得函数
,使得函数 和
和 对其公共定义域上的任意实数
对其公共定义域上的任意实数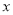 都满足:
都满足: 和
和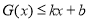 恒成立,则称此直线
恒成立,则称此直线 为
为 和
和 的“隔离直线”,已知函数
的“隔离直线”,已知函数 ,有下列命题:
,有下列命题:
① 在
在 内单调递增;
内单调递增;
② 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的最小值为
的最小值为 ;
;
③ 和
和 之间存在“隔离直线”,且
之间存在“隔离直线”,且 的取值范围是
的取值范围是 ;
;
④ 和
和 之间存在唯一的“隔离直线”
之间存在唯一的“隔离直线” .
.
其中真命题的个数有( )
A. 个 B.
个 B. 个 C.
个 C. 个 D.
个 D. 个
个
 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2015-2016学年广东汕头金山中学高一上学期期中数学试卷(解析版) 题型:解答题
设函数 是定义域为
是定义域为 的奇函数.
的奇函数.
(1)求 的值;
的值;
(2)若 ,求使不等式
,求使不等式 对一切
对一切 恒成立的实数
恒成立的实数 的取值范围;
的取值范围;
(3)若函数 的图象过点
的图象过点 ,是否存在正数
,是否存在正数 ,且
,且 使函数
使函数 在
在 上的最大值为
上的最大值为 ,若存在,求出
,若存在,求出 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源:2016届宁夏吴忠中学高三上第四次月考文科数学试卷(解析版) 题型:解答题
如图,四棱锥 ,平面
,平面 ⊥平面
⊥平面 ,△
,△ 是边长为2的等边三角形,底面
是边长为2的等边三角形,底面 是矩形,且
是矩形,且 .
.

(1)若点 是
是 的中点,求证:
的中点,求证: 平面
平面 ;
;
(2)若 为
为 上任意一点,试问点
上任意一点,试问点 在线段
在线段 上什么位置时,
上什么位置时, ⊥
⊥ ;
;
(3)若点 是
是 的中点,求
的中点,求 .
.
查看答案和解析>>
科目:高中数学 来源:2016届江西省高三上第三次考试理科数学试卷(解析版) 题型:选择题
已知函数 ,(a为常数且
,(a为常数且 ),若
),若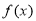 在
在 处取得极值,且
处取得极值,且 ,而
,而 上恒成立,则
上恒成立,则 的取值范围( )
的取值范围( )
A. B.
B.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2016届贵州省高三上学期第三次月考理科数学试卷(解析版) 题型:解答题
在一个盒子中,放有大小相同的红、白、黄三个小球,从中任意摸出一球,若是红球记 分,白球记
分,白球记 分,黄球记
分,黄球记 分.现从这个盒子中,有放回地先后摸出两球,所得分数分别记为
分.现从这个盒子中,有放回地先后摸出两球,所得分数分别记为 ,
, ,设
,设 为坐标原点,点
为坐标原点,点 的坐标为
的坐标为 ,记
,记 .
.
(1)求随机变量 的最大值,并求事件“
的最大值,并求事件“ 取得最大值”的概率;
取得最大值”的概率;
(2)求随机变量 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com