
【题目】已知数列{an},{bn}满足a1=2,b1=4,且 2bn=an+an+1 , an+12=bnbn+1 .
(Ⅰ)求 a 2 , a3 , a4及b2 , b3 , b4;
(Ⅱ)猜想{an},{bn}的通项公式,并证明你的结论;
(Ⅲ)证明:对所有的 n∈N* , ![]()
![]() …
… ![]() <
< ![]() <
< ![]() sin
sin ![]() .
.
【答案】解:(I)令n=1得 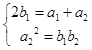 ,解得
,解得 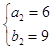 ,
,
令n=2得 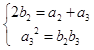 ,解得
,解得 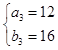 ,
,
令n=3得 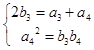 ,解得
,解得 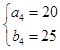 .
.
(II)猜想:an=n(n+1),bn=(n+1)2.
证明:当n=1时,猜想显然成立,
假设n=k(k≥1)猜想成立,即ak=k(k+1),bk=(k+1)2,
∵2bk=ak+ak+1,∴ak+1=2bk﹣ak=2(k+1)2﹣k(k+1)=(k+1)(k+2),
∵ak+12=bkbk+1,∴bk+1= ![]() =(k+2)2,
=(k+2)2,
∴当n=k+1时,猜想成立,
∴an=n(n+1),bn=(n+1)2,n∈N+.
(III)证明:由(II)可知 ![]() =
= ![]() ,
,
于是原不等式等价于 ![]() …
… ![]() <
< ![]() <
< ![]() sin
sin ![]() ,
,
(i)先证 ![]() …
… ![]() <
< ![]() ,
,
∵4n2﹣1<4n2,∴(2n+1)(2n﹣1)<4n2,
∴(2n﹣1)2(2n+1)<4n2(2n﹣1),
即( ![]() )2<
)2< ![]() ,即
,即 ![]() <
< ![]() ,
,
∴ ![]() …
… ![]() <
< ![]()
![]()
![]() …
… ![]() =
= ![]() ,
,
(ii)再证 ![]() <
< ![]() sin
sin ![]() .
.
令 ![]() =x,则0<x≤
=x,则0<x≤ ![]() <
< ![]() ,
,
设f(x)=x﹣ ![]() sinx,则f′(x)=1﹣
sinx,则f′(x)=1﹣ ![]() cosx<0,
cosx<0,
∴f(x)在(0, ![]() )上单调递减,
)上单调递减,
∴f(x)<f(0)=0,即x ![]() sinx,
sinx,
∴ ![]() <
< ![]() sin
sin ![]() .
.
综上,对所有的 n∈N*, ![]()
![]() …
… ![]() <
< 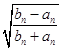 <
< ![]() sin
sin 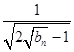
【解析】(I)依次把n=1,2,3代入递推式即可求出{an},{bn}的前4项;(II)利用数学归纳法证明猜想;(III)利用放缩法证明不等式左边,利用函数单调性证明不等式右边.
【考点精析】解答此题的关键在于理解归纳推理的相关知识,掌握根据一类事物的部分对象具有某种性质,退出这类事物的所有对象都具有这种性质的推理,叫做归纳推理.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,正三棱柱ABCA1B1C1中,AB=2,AA1=3,
D为C1B的中点,P为AB边上的动点.
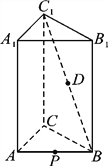
(1)当点P为AB的中点时,证明DP∥平面ACC1A1;
(2)若AP=3PB,求三棱锥BCDP的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在二项式( ![]() +
+ ![]() )n展开式中,前三项的系数成等差数列. 求:(1)展开式中各项系数和;
)n展开式中,前三项的系数成等差数列. 求:(1)展开式中各项系数和;
【答案】解:由题意得2 ![]() ×
× ![]() =1+
=1+ ![]() ×
× ![]() ,
,
化为:n2﹣9n+8=0,解得n=1(舍去)或8.
∴n=8.
在 ![]() 中,令x=1,可得展开式中各项系数和=
中,令x=1,可得展开式中各项系数和= ![]() =
= ![]() .
.
(1)展开式中系数最大的项.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设复数z=2m+(4-m2)i,当实数m取何值时,复数z对应的点:
(1)位于虚轴上?
(2)位于一、三象限?
(3)位于以原点为圆心,以4为半径的圆上?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县农民年均收入服从μ=500元,σ=20元的正态分布,求:
(1)此县农民的年均收入在500~520元之间的人数的百分比;
(2)此县农民的年均收入超过540元的人数的百分比.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4),现从袋中任取一球,X表示所取球的标号.
(1)求X的分布列,均值和方差;
(2)若Y=aX+b,E(Y)=1,D(Y)=11,试求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】直线l过定点P(0,1),且与直线l1:x-3y+10=0,l2:2x+y-8=0分别交于A、B两点.若线段AB的中点为P,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() (
(![]() ,
, ![]() )的图象关于直线
)的图象关于直线![]() 对称,且图像上相邻两个最高点的距离为
对称,且图像上相邻两个最高点的距离为![]() .
.
(1)求函数![]() 的解析式以及它的单调递增区间;
的解析式以及它的单调递增区间;
(2)是否存在实数![]() ,满足不等式
,满足不等式 ?若存在,求出
?若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com