练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】袋中有20个大小相同的球，其中记上0号的有10个，记上n号的有n个（n＝1,2,3,4），现从袋中任取一球，X表示所取球的标号.

    （1）求X的分布列，均值和方差；

    （2）若Y＝aX＋b，E（Y）＝1，D（Y）＝11，试求a，b的值．

    【答案】见解析

    【解析】（1）X的分布列为：

    X

    0

    1

    2

    3

    4

    P

    故E（X）＝0×＋1×＋2×＋3×＋4×＝1.5，D（X）＝（0－1.5）2×＋（1－1.5）2×＋（2－1.5）2×＋（3－1.5）2×＋（4－1.5）2×＝2.75.

    （2）由D（Y）＝a2D（X），得a2×2.75＝11，即a＝±2，又E（Y）＝aE（X）＋b，

    故当a＝2时，1＝1.5×2＋b，解得b＝－2；

    当a＝－2时，1＝－2×1.5＋b，解得b＝4.

    因此，或

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某城市随机抽取一年（365天）内100天的空气质量指数的检测数据，结果统计如下：

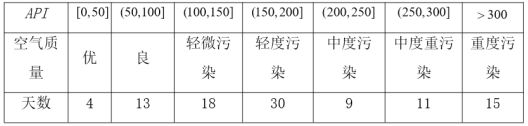
    记某企业每天由空气污染造成的经济损失（单位：元），空气质量指数为．在区间对企业没有造成经济损失；在区间对企业造成经济损失成直线模型（当为150时造成的经济损失为500元，当为200时，造成的经济损失为700元）；当大于300时造成的经济损失为2000元．

    （1）试写出的表达式；

    （2）试估计在本年内随机抽取一天，该天经济损失大于200元且不超过600元的概率；

    （3）若本次抽取的样本数据有30天是在供暖季，其中有8天为重度污染，完成下面列联表，并判断

    能否有的把握认为该市本年空气重度污染与供暖有关？

    附：

    0.25

    0.15

    0.10

    0.05

    0.025

    0.010

    0.005

    0.001

    1.32

    2.07

    2.70

    3.74

    5.02

    6.63

    7.87

    10.82

    非重度污染

    重度污染

    合计

    供暖季

    非供暖季

    合计

    100

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知不等式的解集为，

    (1)求；

    (2)解不等式.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （1）若关于的方程在区间上有两个不同的解．

    （ⅰ）求的取值范围；

    （ⅱ）若，求的取值范围；

    （2）设函数在区间上的最大值和最小值分别为，求的表达式．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为推行“微课、翻转课堂”教学法，某数学老师分别用传统教学和“微课、翻转课堂”两种不同的教学方式，在甲、乙两个平行班级进行教学实验，为了比较教学效果，期中考试后，分别从两个班级中各随机抽取20名学生的成绩进行统计，结果如下表：

    记成绩不低于70分者为“成绩优良”．

    （1）由以上统计数据填写下面列联表，并判断“成绩优良与教学方式是否有关”？

    附：

    临界值表：

    （2）现从上述40人中，学校按成绩是否优良采用分层抽样的方法抽取8人进行考核，在这8人中，记成绩不优良的乙班人数为，求的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在平行四边形中，，四边形为直角梯形，∥,，, 平面平面.

    (1)求证：；

    （2）求平面与平面所成锐二面角的余弦值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，点E为正方形ABCD边CD上异于点C，D的动点，将△ADE沿AE翻折成△SAE，使得平面SAE⊥平面ABCE，则下列三个说法中正确的个数是（ ）

    ①存在点E使得直线SA⊥平面SBC

    ②平面SBC内存在直线与SA平行

    ③平面ABCE内存在直线与平面SAE平行

    A．0 B．1 C．2 D．3

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设数列的前项和为，点均在函数的图象上.

    (1)求证：数列为等差数列；

    (2)设是数列的前项和，求使对所有都成立的最小正整数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知在锐角△ABC中，两向量p＝(2－2sin A，cos A＋sin A)，q＝(sin A－cos A,1＋sin A)，且p与q是共线向量.

    （1）求A的大小；

    （2）求函数y＝2sin2B＋cos（）取最大值时，角B的大小.

    查看答案和解析>>

    同步练习册答案