
【题目】已知函数![]() .
.
(1)若关于![]() 的方程
的方程![]() 在区间
在区间![]() 上有两个不同的解
上有两个不同的解![]() .
.
(ⅰ)求![]() 的取值范围;
的取值范围;
(ⅱ)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)设函数![]() 在区间
在区间![]() 上的最大值和最小值分别为
上的最大值和最小值分别为![]() ,求
,求![]() 的表达式.
的表达式.
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:
【题目】某种商品原来每件售价为25元,年销售8万件.
(1)据市场调查,若价格每提高1元,销售量将相应减少2000件,要使销售的总收入不低于原收入,该商品每件定价最多为多少元?
(2)为了扩大该商品的影响力,提高年销售量,公司决定明年对该商品进行全面技术革新和营销策略改革,并提高定价到![]() 元,公司拟投入
元,公司拟投入![]() 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入![]() 作为浮动宣传费用.试问:当该商品明年的销售量
作为浮动宣传费用.试问:当该商品明年的销售量![]() 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]()
![]() ,若函数
,若函数![]() 的图象与x轴的任意两个相邻交点间的距离为
的图象与x轴的任意两个相邻交点间的距离为![]() ,当
,当![]() 时,函数
时,函数![]() 取得最大值
取得最大值![]() .
.
(1)求函数![]() 的解析式,并写出它的单调增区间;
的解析式,并写出它的单调增区间;
(2)若![]() ,求函数
,求函数![]() 的值域.
的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,AB=AD,∠BAD=60°,E,F分别是AP,AD的中点.
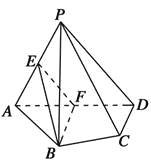
求证:(1)直线EF∥平面PCD;
(2)平面BEF⊥平面PAD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋中有20个大小相同的球,其中记上0号的有10个,记上n号的有n个(n=1,2,3,4),现从袋中任取一球,X表示所取球的标号.
(1)求X的分布列,均值和方差;
(2)若Y=aX+b,E(Y)=1,D(Y)=11,试求a,b的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]()
![]() 的一个焦点与抛物线
的一个焦点与抛物线![]() 的焦点重合,点
的焦点重合,点![]() 在
在![]() 上
上
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)直线![]() 不过原点O且不平行于坐标轴,
不过原点O且不平行于坐标轴,![]() 与
与![]() 有两个交点
有两个交点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,证明:
,证明:![]() 的斜率与直线
的斜率与直线![]() 的斜率的乘积为定值.
的斜率的乘积为定值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com