
| A. | (0,4$\sqrt{2}$) | B. | (1,4) | C. | (-∞,4$\sqrt{2}$) | D. | ($\sqrt{2}$,4) |
分析 求导数,分离参数,再求导数,确定函数值的范围,即可求出实数a的取值范围.
解答 解:∵函数f(x)=a$\sqrt{x+1}$+$\frac{1}{x}$,
∴f′(x)=$\frac{a}{2\sqrt{x+1}}$-$\frac{1}{{x}^{2}}$=0,
∴a=$\frac{2\sqrt{x+1}}{{x}^{2}}$,
∴a′=$\frac{-x(3x+4)}{\sqrt{x+1}}$•$\frac{1}{{x}^{4}}$,
∵x∈(-1,-$\frac{1}{2}$),
∴a′>0,
∴函数单调递增,
∴0<a<4$\sqrt{2}$.
故选:A.
点评 本题考查了导数的综合应用,考查函数的极值,考查学生的计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | -5 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在⊙O的直径AB的延长线上取点P,作⊙O的切线PN,N为切点,在AB上找一点M,使PN=PM,连接NM并延长交⊙O于点C.
如图,在⊙O的直径AB的延长线上取点P,作⊙O的切线PN,N为切点,在AB上找一点M,使PN=PM,连接NM并延长交⊙O于点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
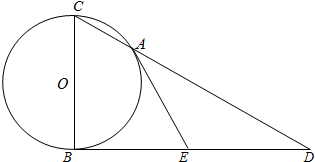 如图,过⊙O外一点E作⊙O的两条切线EA、EB,其中A、B为切点,BC为⊙O的一条直径,连CA并延长交BE的延长线于D点.
如图,过⊙O外一点E作⊙O的两条切线EA、EB,其中A、B为切点,BC为⊙O的一条直径,连CA并延长交BE的延长线于D点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
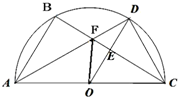 如图所示,AC为⊙O的直径,E为BC的中点,延长OE与⊙O相交于点D,连结AD,DC,F为BC与AD的交点.
如图所示,AC为⊙O的直径,E为BC的中点,延长OE与⊙O相交于点D,连结AD,DC,F为BC与AD的交点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
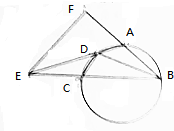 如图,A、B、C、D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.
如图,A、B、C、D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com