
 如图,在⊙O的直径AB的延长线上取点P,作⊙O的切线PN,N为切点,在AB上找一点M,使PN=PM,连接NM并延长交⊙O于点C.
如图,在⊙O的直径AB的延长线上取点P,作⊙O的切线PN,N为切点,在AB上找一点M,使PN=PM,连接NM并延长交⊙O于点C.分析 (1)连接ON,运用圆的切线的性质和等腰三角形的性质,由垂直的判定即可得证;
(2)运用直角三角形的勾股定理和圆的相交弦定理,计算即可得到所求值.
解答 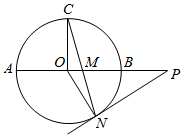 解:(1)证明:连接ON,则ON⊥PN,且△OCN为等腰三角形,
解:(1)证明:连接ON,则ON⊥PN,且△OCN为等腰三角形,
则∠OCN=∠ONC,∵PN=PM,
∴∠PMN=∠PNM,∵∠OCM+∠OMC=∠ONC+∠PNM=90°,
∴∠COM=90°,∴OC⊥AB.
(2)在Rt△ONP中,由于OM=MP,
∴OP2=PN2+ON2,∴${(2PM)^2}=P{N^2}+{(2\sqrt{3})^2}$,
∴4PN2=PN2+12,∴PN=2,从而$OP=\sqrt{{2^2}+{{(2\sqrt{3})}^2}}=4$,
∴$OM=2,BM=OB-OM=2\sqrt{3}-2,AM=OA+OM=2\sqrt{3}+2$,
由相交弦定理可得MN•CM=BM•AM,又$CM=\sqrt{(2\sqrt{3}{)^2}+{2^2}}=4$,
∴$MN=\frac{BM•AM}{CM}=\frac{{(2\sqrt{3}-2)(2\sqrt{3}+2)}}{4}=2$.
点评 本题主要考查圆的切线性质和圆的相交弦定理,及勾股定理的运用,考查推理和运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 1 | C. | $-\sqrt{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
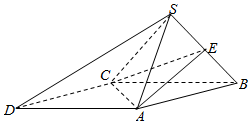 如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,点E是SB的中点,∠SBC=45°,SC=SB=2$\sqrt{2}$,△ACD为等边三角形.
如图,在四棱锥S-ABCD中,底面ABCD为平行四边形,侧面SBC⊥底面ABCD,点E是SB的中点,∠SBC=45°,SC=SB=2$\sqrt{2}$,△ACD为等边三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
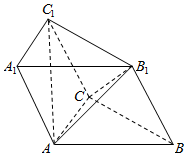 如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.
如图,已知斜三棱柱ABC-A1B1C1中,底面ABC是等边三角形,侧面BB1C1C是菱形,∠B1BC=60°.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,4$\sqrt{2}$) | B. | (1,4) | C. | (-∞,4$\sqrt{2}$) | D. | ($\sqrt{2}$,4) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com