
分析 (1)分别利用f(-2)≤4和f(2)≤4求解绝对值的不等式得到a的范围,取交集得答案;
(2)利用绝对值的不等式求得f(x)的最小值为M,得到$\frac{1}{m}$+$\frac{2}{n}$=2,再由基本不等式求得m+2n的最小值.
解答 解:(1)由f(2)=3+|a-2|≤4,得|a-2|≤1,即1≤a≤3.
由f(-2)=1+|a+2|≤4,得|a+2|≤3,即-5≤a≤1.
∵f(-2)≤4和f(2)≤4同时成立,
∴a=1;
(2)∵f(x)=|x+1|+|x-a|=|x+1|+|x-1|≥|(x+1)-(x-1)|=2,
当且仅当(x+1)(x-1)≤0,即-1≤x≤1时取等号,∴M=2.
即$\frac{1}{m}$+$\frac{2}{n}$=2(m,n∈R*),
∴m+2n=$\frac{1}{2}(m+2n)(\frac{1}{m}+\frac{2}{n})=\frac{1}{2}(1+4+\frac{2n}{m}+\frac{2m}{n})$$≥\frac{1}{2}(5+2\sqrt{4})=\frac{9}{2}$.
当且仅当$\frac{2n}{m}=\frac{2m}{n}$且$\frac{1}{m}+\frac{2}{n}=2$,即m=n=$\frac{3}{2}$时取等号.
∴m+2n的最小值为$\frac{9}{2}$.
点评 本题考查绝对值不等式的解法,训练了利用不等式求最小值,是中档题.


科目:高中数学 来源: 题型:解答题
 如图,在⊙O的直径AB的延长线上取点P,作⊙O的切线PN,N为切点,在AB上找一点M,使PN=PM,连接NM并延长交⊙O于点C.
如图,在⊙O的直径AB的延长线上取点P,作⊙O的切线PN,N为切点,在AB上找一点M,使PN=PM,连接NM并延长交⊙O于点C.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
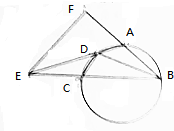 如图,A、B、C、D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.
如图,A、B、C、D四点在同一圆上,BC与AD的延长线交于点E,点F在BA的延长线上.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
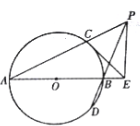 如图,AB是⊙O的直径,弦DB、AC的延长线相交于点P,PE垂直于AB的延长线于点E.
如图,AB是⊙O的直径,弦DB、AC的延长线相交于点P,PE垂直于AB的延长线于点E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
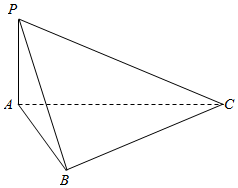 如图,在三棱锥P-ABC中,已知PA⊥平面ABC,平面PAB⊥平面PBC
如图,在三棱锥P-ABC中,已知PA⊥平面ABC,平面PAB⊥平面PBC查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{x^2}{16}+\frac{y^2}{9}=1$ | B. | $\frac{x^2}{9}+\frac{y^2}{16}=1$ | C. | $\frac{x^2}{25}+\frac{y^2}{16}=1$ | D. | $\frac{x^2}{16}+\frac{y^2}{25}=1$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com