
【题目】定义在[-1,1]上的偶函数f(x),已知当x∈[0,1]时的解析式为![]() (a∈R).
(a∈R).
(1)求f(x)在[-1,0]上的解析式;
(2)求f(x)在[0,1]上的最大值h(a).
 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:
【题目】设O为坐标原点,动点M在椭圆C![]() 上,过M作x轴的垂线,垂足为N,点P满足
上,过M作x轴的垂线,垂足为N,点P满足![]() .
.
(1)求点P的轨迹方程;
(2)设点![]() 在直线
在直线![]() 上,且
上,且![]() .证明:过点P且垂直于OQ的直线
.证明:过点P且垂直于OQ的直线![]() 过C的左焦点F.
过C的左焦点F.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个不透明的盒子中关有蝴蝶、蜜蜂和蜻蜓三种昆虫共11只,现在盒子上开一小孔,每次只能飞出1只昆虫(假设任意1只昆虫等可能地飞出).若有2只昆虫先后任意飞出(不考虑顺序),则飞出的是蝴蝶或蜻蜓的概率是![]() .
.
(1)求盒子中蜜蜂有几只;
(2)若从盒子中先后任意飞出3只昆虫(不考虑顺序),记飞出蜜蜂的只数为X,求随机变量X的分布列与数学期望E(X).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() 分别为椭圆的左、右焦点,点
分别为椭圆的左、右焦点,点![]() 在椭圆上,当
在椭圆上,当![]() 时,
时, ![]() 内切圆的半径为
内切圆的半径为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)已知直线![]() 与椭圆
与椭圆![]() 相较于
相较于![]() 两点,且
两点,且![]() ,当直线
,当直线![]() 的斜率之和为2时,问:点
的斜率之和为2时,问:点![]() 到直线
到直线![]() 的距离是否存在最大值?若存在,求出最大值;若不存在,说明理由.
的距离是否存在最大值?若存在,求出最大值;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大学餐饮中心为了了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品 | 不喜欢甜品 | 合计 | |
南方学生 | 60 | 20 | 80 |
北方学生 | 10 | 10 | 20 |
合计 | 70 | 30 | 100 |
![]() 根据表中数据,问是否有
根据表中数据,问是否有![]() 的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
![]() 已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱柱![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
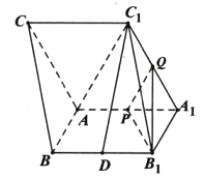
(1)设棱![]() 的中点为
的中点为![]() ,证明:
,证明:![]() 平面
平面![]() ;
;
(2)若![]() ,
,![]() ,
,![]() ,且平面
,且平面![]() 平面
平面![]() .
.
(i)求三棱柱![]() 的体积
的体积![]() ;
;
(ii)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司计划在甲、乙两个电视台做总时间不超过 300 分钟的广告,广告总费用不超过9万元.甲、乙电视台的广告收费标准分别为500元/分钟和200元/分钟.甲、乙两个电视台为该公司所做的每分钟广告,能给公司带来的收益分别为0.3万元和0.2万元.设该公司在甲、乙两个电视台做广告的时间分别为![]() 分钟和
分钟和![]() 分钟.
分钟.
(Ⅰ)用![]() 列出满足条件的数学关系式,并画出相应的平面区域;
列出满足条件的数学关系式,并画出相应的平面区域;
(Ⅱ)该公司如何分配在甲、乙两个电视台做广告的时间使公司的收益最大,并求出最大收益是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com