
【题目】某大型公司为了切实保障员工的健康安全,贯彻好卫生防疫工作的相关要求,决定在全公司范围内举行一次![]() 普查,为此需要抽验1000人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
普查,为此需要抽验1000人的血样进行化验,由于人数较多,检疫部门制定了下列两种可供选择的方案.
方案①:将每个人的血分别化验,这时需要验1000次.
方案②:按![]() 个人一组进行随机分组,把从每组
个人一组进行随机分组,把从每组![]() 个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这
个人抽来的血混合在一起进行检验,如果每个人的血均为阴性,则验出的结果呈阴性,这![]() 个人的血只需检验一次(这时认为每个人的血化验
个人的血只需检验一次(这时认为每个人的血化验![]() 次);否则,若呈阳性,则需对这
次);否则,若呈阳性,则需对这![]() 个人的血样再分别进行一次化验,这样,该组
个人的血样再分别进行一次化验,这样,该组![]() 个人的血总共需要化验
个人的血总共需要化验![]() 次.
次.
假设此次普查中每个人的血样化验呈阳性的概率为![]() ,且这些人之间的试验反应相互独立.
,且这些人之间的试验反应相互独立.
(1)设方案②中,某组![]() 个人的每个人的血化验次数为
个人的每个人的血化验次数为![]() ,求
,求![]() 的分布列;
的分布列;
(2)设![]() ,试比较方案②中,
,试比较方案②中,![]() 分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
分别取2,3,4时,各需化验的平均总次数;并指出在这三种分组情况下,相比方案①,化验次数最多可以平均减少多少次?(最后结果四舍五入保留整数)
【答案】(1)详解见解析;(2)690,604,594;406.
【解析】
(1)设每个人的血呈阴性反应的概率为![]() ,依题意知
,依题意知![]() 的可能取值,计算分布列即可;
的可能取值,计算分布列即可;
(2)方案②中计算每个人的平均化验次数![]() ,分别求出
,分别求出![]() 、3、4时
、3、4时![]() 的值,再与方案①比较,即可得出所求.
的值,再与方案①比较,即可得出所求.
解:(1)由题可知,每个人的血样化验呈阳性的概率为![]() ,
,
设每个人的血呈阴性反应的概率为![]() ,则
,则![]() ,
,
所以![]() 个人的混合后呈阴性的概率为
个人的混合后呈阴性的概率为![]() ,呈阳性反应的概率为
,呈阳性反应的概率为![]() ,
,
依题意知![]() 的可能取值为
的可能取值为![]() ,
,![]() ,
,
所以![]() 的分布列为;
的分布列为;
|
|
|
|
|
|
(2)方案②中,结合(1)知每个人的平均化验次数为:
![]() ;
;
所以当![]() 时,
时,![]() ,
,
此时1000人需要化验的总次数为690次;
当![]() 时,
时,![]() ,
,
此时1000人需要化验的总次数为604次;
当![]() 时,
时,![]() ,
,
此时1000人需要化验的总次数为594次;
即![]() 时化验次数最多,
时化验次数最多,![]() 时化验次数居中,
时化验次数居中,![]() 时化验次数最少,
时化验次数最少,
而采用方案①需要化验1000次,
所以在这三种分组情况下,相比方案①,
![]() 时化验次数最多可以平均减少
时化验次数最多可以平均减少![]() (次
(次![]() .
.


科目:高中数学 来源: 题型:
【题目】2019年12月12日我国出现了新型冠状病毒所感染的肺炎,新型冠状病毒的传染性极强.下图是2020年1月26号到2月17号全国/湖北/非湖北新增新型冠状病毒感染确诊病例对比图,根据图象下列判断错误的是( )
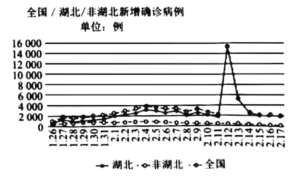
A.该时段非湖北新增感染确诊病例比湖北少
B.全国新增感染确诊病例平均数先增后减
C.2.12全国新增感染确诊病例明显增加,主要是由湖北引起的
D.2.12全国新增感染确诊病例数突然猛增,不会影响该段时期全国新增病例数的中位数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() ,圆
,圆![]() ,如图,
,如图,![]() 分别交
分别交![]() 轴正半轴于点
轴正半轴于点![]() .射线
.射线![]() 分别交
分别交![]() 于点
于点![]() ,动点
,动点![]() 满足直线
满足直线![]() 与
与![]() 轴垂直,直线
轴垂直,直线![]() 与
与![]() 轴垂直.
轴垂直.

(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 作直线
作直线![]() 交曲线
交曲线![]() 与点
与点![]() ,射线
,射线![]() 与点
与点![]() ,且交曲线
,且交曲线![]() 于点
于点![]() .问:
.问:![]() 的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
的值是否是定值?如果是定值,请求出该定值;如果不是定值,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为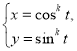
![]() 为参数
为参数![]() .以坐标原点为极点,
.以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)当![]() 时,
时,![]() 是什么曲线?
是什么曲线?
(2)当![]() 时,求
时,求![]() 与
与![]() 的公共点的直角坐标.
的公共点的直角坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com