
【题目】已知cos(π+α) ![]() =
= ![]() ,且
,且 ![]() <α<
<α< ![]() ,求sin α与cos α的值.
,求sin α与cos α的值.
【答案】解:cos(π+α)=﹣cos α, ![]() =﹣sin α. ∴sin αcos α=
=﹣sin α. ∴sin αcos α= ![]() ,即2sin αcos α=
,即2sin αcos α= ![]() ①
①
又∵sin2α+cos2α=1,②
②+①得(sin α+cos α)2= ![]() ,
,
②-①得(sin α﹣cos α)2= ![]() ,
,
又∵ ![]() <α<
<α< ![]() ,
,
∴sin α>cos α>0,
即sin α+cos α>0,sin α﹣cos α>0,
∴sin α+cos α= ![]() ,③
,③
sin α﹣cos α= ![]() ,④
,④
③+④得sin α= ![]() ,③-④得cos α=
,③-④得cos α= ![]()
【解析】由已知利用诱导公式可求2sin αcos α= ![]() ,结合同角三角函数基本关系式可求:(sin α+cos α)2=
,结合同角三角函数基本关系式可求:(sin α+cos α)2= ![]() ,(sin α﹣cos α)2=
,(sin α﹣cos α)2= ![]() ,结合α的范围可求sin α+cos α>0,sin α﹣cos α>0,可求sin α+cos α=
,结合α的范围可求sin α+cos α>0,sin α﹣cos α>0,可求sin α+cos α= ![]() ,sin α﹣cos α=
,sin α﹣cos α= ![]() ,联立即可得解.
,联立即可得解.
【考点精析】解答此题的关键在于理解两角和与差的正弦公式的相关知识,掌握两角和与差的正弦公式:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为 ![]() ,b=
,b= ![]() .
.
(1)求椭圆C的标准方程;
(2)F1 , F2分别为椭圆的左、右焦点,A、B为椭圆的左、右顶点,P为椭圆C上的点,求证:以PF2为直径的圆与以AB为直径的圆相切;
(3)过左焦点F1作互相垂直的弦MN与GH,判断MN的中点与GH的中点所在直线l是否过x轴上的定点,如果是,求出定点坐标,如果不是,说出理由. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个盒子装有六张卡片,上面分别写着如下六个函数:
![]()
![]()
![]()
![]()
![]()
![]() .
.
(Ⅰ)从中任意拿取![]() 张卡片,其中至少有一张卡片上写着的函数为奇函数,在此条件下,求两张卡片上写着的函数相加得到的新函数为奇函数的概率;
张卡片,其中至少有一张卡片上写着的函数为奇函数,在此条件下,求两张卡片上写着的函数相加得到的新函数为奇函数的概率;
(Ⅱ)现从盒子中逐一抽取卡片,且每次取出后均不放回,若取到一张写有偶函数的卡片则停止抽取,否则继续进行,求抽取次数![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为缓解高三学生的高考压力,经常举行一些心理素质综合能力训练活动,经过一段时间的训练后从该年级800名学生中随机抽取100名学生进行测试,并将其成绩分为![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 五个等级,统计数据如图所示(视频率为概率),根据以上抽样调查数据,回答下列问题:
五个等级,统计数据如图所示(视频率为概率),根据以上抽样调查数据,回答下列问题:
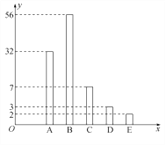
(1)试估算该校高三年级学生获得成绩为![]() 的人数;
的人数;
(2)若等级![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 分别对应100分、90分、80分、70分、60分,学校要求平均分达90分以上为“考前心理稳定整体过关”,请问该校高三年级目前学生的“考前心理稳定整体”是否过关?
分别对应100分、90分、80分、70分、60分,学校要求平均分达90分以上为“考前心理稳定整体过关”,请问该校高三年级目前学生的“考前心理稳定整体”是否过关?
(3)为了解心理健康状态稳定学生的特点,现从![]() 、
、![]() 两种级别中,用分层抽样的方法抽取11个学生样本,再从中任意选取3个学生样本分析,求这3个样本为
两种级别中,用分层抽样的方法抽取11个学生样本,再从中任意选取3个学生样本分析,求这3个样本为![]() 级的个数
级的个数![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】△ABC中,a、b、c分别为∠A,∠B,∠C的对边,如果a、b、c成等差数列,∠B=30°,△ABC的面积为 ![]() ,那么b等于( )
,那么b等于( )
A.![]()
B.1+ ![]()
C.![]()
D.2+ ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
: ![]() 的焦点
的焦点![]() 也是椭圆
也是椭圆![]() :
: ![]() (
(![]() )的一个焦点,
)的一个焦点, ![]() 与
与![]() 的公共弦长为
的公共弦长为![]() .
.
(Ⅰ)求![]() 的方程
的方程
(Ⅱ)过点![]() 的直线
的直线![]() 与
与![]() 相交于
相交于![]() ,
, ![]() 两点,与
两点,与![]() 相交于
相交于![]() ,
, ![]() 两点,且
两点,且![]() ,
, ![]() 同向.若
同向.若![]() 求直线
求直线![]() 的斜率;
的斜率;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com