
【题目】如图,三棱柱![]() 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是![]() ,
, ![]() 是
是![]() 的中点.
的中点.
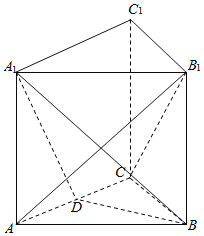
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
【题目】随着社会发展,淮北市在一天的上下班时段也出现了堵车严重的现象。交通指数是交通拥堵指数的简称,是综合反映道路网畅通或拥堵的概念.记交通指数为T,其范围为[0,10],分别有5个级别:T∈[0,2)畅通;T∈[2,4)基本畅通;T∈[4,6)轻度拥堵;T∈[6,8)中度拥堵;T∈[8,10]严重拥堵.早高峰时段(T≥3 ),从淮北市交通指挥中心随机选取了一至四马路之间50个交通路段,依据交通指数数据绘制的直方图如图所示:
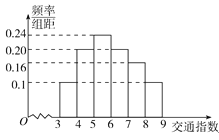
(I)据此直方图估算交通指数T∈[4,8)时的中位数和平均数;
(II)据此直方图求出早高峰一至四马路之间的3个路段至少有2个严重拥堵的概率是多少?
(III)某人上班路上所用时间若畅通时为20分钟,基本畅通为30分钟,轻度拥堵为35分钟,中度拥堵为45分钟,严重拥堵为60分钟,求此人用时间的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=Asin( ![]() x+φ),x∈R,A>0,0<φ<
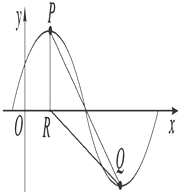
x+φ),x∈R,A>0,0<φ< ![]() .y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ=
.y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ= ![]() .
. 
(1)求f(x)的最小正周期以及解析式.
(2)用五点法画出f(x)在x∈[﹣ ![]() ,
, ![]() ]上的图象.
]上的图象.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在一次抽样调查中测得样本的6组数据,得到一个变量![]() 关于
关于![]() 的回归方程模型,其对应的数值如下表:
的回归方程模型,其对应的数值如下表:
| 2 | 3 | 4 | 5 | 6 | 7 |
|
|
|
|
|
|
|
(1)请用相关系数![]() 加以说明
加以说明![]() 与
与![]() 之间存在线性相关关系(当
之间存在线性相关关系(当![]() 时,说明
时,说明![]() 与
与![]() 之间具有线性相关关系);
之间具有线性相关关系);
(2)根据(1)的判断结果,建立![]() 关于
关于![]() 的回归方程并预测当
的回归方程并预测当![]() 时,对应的
时,对应的![]() 值为多少(
值为多少(![]() 精确到
精确到![]() ).
).
附参考公式:回归方程![]() 中斜率和截距的最小二乘法估计公式分别为:
中斜率和截距的最小二乘法估计公式分别为:
 ,
,![]() ,相关系数
,相关系数![]() 公式为:
公式为: .
.
参考数据:
![]() ,
,![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列五个命题:①“若![]() ,则
,则![]() 或
或![]() ”是假命题;②从正方体的面对角线中任取两条作为一对,其中所成角为
”是假命题;②从正方体的面对角线中任取两条作为一对,其中所成角为![]() 的有48对;③“
的有48对;③“ ![]() ”是方程
”是方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线的充分不必要条件;④点
轴上的双曲线的充分不必要条件;④点![]() 是曲线
是曲线![]() (
(![]() ,
, ![]() )上的动点,且满足
)上的动点,且满足![]() ,则
,则![]() 的取值范围是
的取值范围是![]() ;⑤若随机变量
;⑤若随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .其中正确命题的序号是__________(请把正确命题的序号填在横线上).
.其中正确命题的序号是__________(请把正确命题的序号填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界)。
(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率;
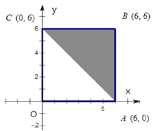
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com