
【题目】已知函数f(x)=Asin( ![]() x+φ),x∈R,A>0,0<φ<
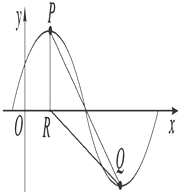
x+φ),x∈R,A>0,0<φ< ![]() .y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ=
.y=f(x)的部分图象如图所示,P、Q 分别为该图象的最高点和最低点,点P的坐标为(1,A).点R的坐标为(1,0),∠PRQ= ![]() .
. 
(1)求f(x)的最小正周期以及解析式.
(2)用五点法画出f(x)在x∈[﹣ ![]() ,
, ![]() ]上的图象.
]上的图象.
【答案】
(1)解:由题意得:f(x)的最小正周期 ![]() ,
,
因为P(1,A)在 ![]() 的图象上,
的图象上,
所以 ![]() ,
,
所以 ![]() ,即
,即 ![]() ,
,
又因为 ![]() ,
,
因此, ![]()
过Q做QD⊥x轴,垂足为D,设D(x0,0),则Q(x0,﹣A),由周期为6可知,RD=3,
由于 ![]() ,
,
所以 ![]() ,于是QD=RD=3,
,于是QD=RD=3,
所以A=3,
∴ ![]()
(2)解:列表如下:
x | ﹣0.5 | 1 | 2.5 | 4 | 5.5 |
| 0 |
| π |
| 2π |
| 0 | 3 | 0 | ﹣3 | 0 |
描点连线,作图如下:
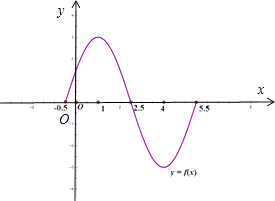
【解析】(1)根据周期公式求出函数f(x)的最小正周期,由P(1,A)在 ![]() 的图象上,结合范围0<φ<
的图象上,结合范围0<φ< ![]() ,可求φ,由图象和条件设出点Q的坐标,再过点Q做x轴的垂线,设垂足为D,根据条件和正切函数求出A,从而可得函数解析式;(2)利用五点作图法即可作图得解.
,可求φ,由图象和条件设出点Q的坐标,再过点Q做x轴的垂线,设垂足为D,根据条件和正切函数求出A,从而可得函数解析式;(2)利用五点作图法即可作图得解.
【考点精析】认真审题,首先需要了解五点法作函数y=Asin(ωx+φ)的图象(描点法及其特例—五点作图法(正、余弦曲线),三点二线作图法(正、余切曲线)).


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明: 
(1)CD=BC;
(2)△BCD∽△GBD.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在某港口![]() 处获悉,其正东方向距离20n mile的
处获悉,其正东方向距离20n mile的![]() 处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°距港口10n mile的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船.
处有一艘渔船遇险等待营救,此时救援船在港口的南偏西30°距港口10n mile的C处,救援船接到救援命令立即从C处沿直线前往B处营救渔船.
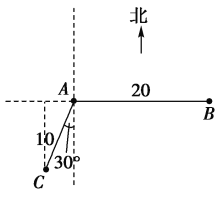
(1)求接到救援命令时救援船距渔船的距离;
(2)试问救援船在C处应朝北偏东多少度的方向沿直线前往B处救援?(已知![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位有工程师6人,技术员12人,技工18人,要从这些人中取一个容量为n的样本;如果采用系统抽样和分层抽样方法抽取,无须剔除个体;如果样本容量增加1个,则在采用系统抽样时需要在总体中先剔除一个个体,则n的值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列四个结论:
①若α、β为第一象限角,且α>β,则sinα>sinβ
②函数y=|sinx|与y=|tanx|的最小正周期相同
③函数f(x)=sin(x+ ![]() )在[﹣
)在[﹣ ![]() ,
, ![]() ]上是增函数;
]上是增函数;
④若函数f(x)=asinx﹣bcosx的图象的一条对称轴为直线x= ![]() ,则a+b=0.
,则a+b=0.
其中正确结论的序号是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
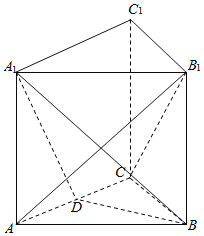
【题目】如图,三棱柱![]() 的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是
的底面是边长为2的正三角形且侧棱垂直于底面,侧棱长是![]() ,
, ![]() 是
是![]() 的中点.
的中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,焦点为
,焦点为![]() ,点
,点![]() 在抛物线
在抛物线![]() 上,且
上,且![]() 到
到![]() 的距离比
的距离比![]() 到直线
到直线![]() 的距离小1.
的距离小1.
(1)求抛物线![]() 的方程;
的方程;
(2)若点![]() 为直线
为直线![]() 上的任意一点,过点
上的任意一点,过点![]() 作抛物线
作抛物线![]() 的切线
的切线![]() 与
与![]() ,切点分别为
,切点分别为![]() ,求证:直线
,求证:直线![]() 恒过某一定点.
恒过某一定点.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com