解法一:(1)∵AC
1是正方体,∴AD⊥面DC
1.
又D
1F?面DC
1,∴AD⊥D
1F.
(2)取AB中点G,连接A
1G,FG.
因为F是CD的中点,所以GF、AD平行且相等,
又A
1D
1、AD平行且相等,所以GF、A
1D
1平行且相等,故GFD
1A
1是平行四边形,A
1G∥D
1F.
设A
1G与AE相交于点H,则∠AHA
1是AE与D
1F所成的角,
因为E是BB
1的中点,所以Rt△A
1AG≌Rt△ABE,
∴∠GA
1A=∠GAH,从而∠AHA
1=90°,即直线AE与D
1F所成角为直角.
(3)由(1)知AD⊥D
1F,由(2)知AE⊥D
1F,
又AD∩AE=A,所以D
1F⊥面AED.
又因为D
1F?面A
1FD
1,
所以面AED⊥面A
1FD
1.
(4)连接GE,GD
1.
∵FG∥A
1D
1,∴FG∥面A
1ED
1,
∵AA
1=2,
∴面积S
△A1GE=S
ABB1A1-2S
△A1AG-S
△GBE=

又
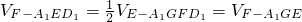
=
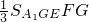
∴
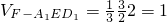
解法二:利用用向量求解
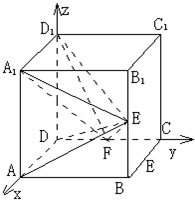
解:设正方体的棱长为2,以D为原点,DA为x轴,DC为y轴,DD
1为z轴建立空间直角坐标系,
则D(0,0,0),A(2,0,0),F(0,1,0),E(2,2,1),A
1(2,0,2),D
1(0,0,2),
(1)∵
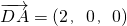
,

,得
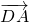
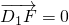
,∴AD⊥D
1F;
(2)又
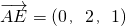
,得
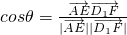
=
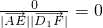
∴AE与D
1F所成的角为90°
(3)由题意:
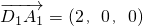
,
设平面AED的法向量为
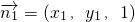
,设平面A
1FD
1的法向量为

,
由
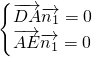
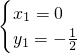
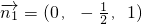
由
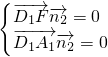
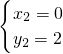
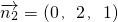
得
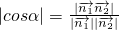
=
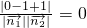
∴面AED⊥面A
1FD
1.
(4)∵AA
1=2,
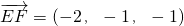
,
平面A
1FD
1的法向量为
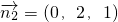
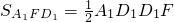
=

,
∴E到平面A
1FD
1的距离
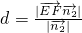
=
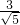
,
∴
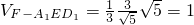
.
分析:解法一:传统证法.(1)利用线面垂直,证明线线垂直;
(2)设A
1G与AE相交于点H,先证∠AHA
1是AE与D
1F所成的角,再求直线AE与D
1F所成角;
(3)利用线面垂直,证明面面垂直;
(4)利用转换底面的方法,求三棱锥的体积;
解法二:向量证法.设正方体的棱长为2,以D为原点,DA为x轴,DC为y轴,DD
1为z轴建立空间直角坐标系,
则D(0,0,0),A(2,0,0),F(0,1,0),E(2,2,1),A
1(2,0,2),D
1(0,0,2),
(1)利用
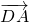
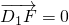
,可证AD⊥D
1F;
(2)求得
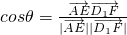
=
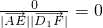
,可求AE与D
1F所成的角;(3)由题意:
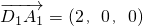
,
设平面AED的法向量为
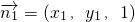
,设平面A
1FD
1的法向量为

,证明平面的法向量垂直,即可证明面AED⊥面A
1FD
1.
(4)先求得
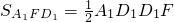
=

,计算E到平面A
1FD
1的距离
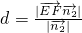
=
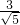
,即可求三棱锥的体积.
点评:本题重点考查线面垂直、面面垂直,考查三棱锥的体积,两法并用,注意比较,细细体会.

 如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
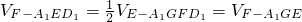 =
=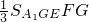
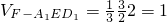
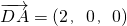 ,
, ,得
,得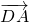
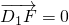 ,∴AD⊥D1F;
,∴AD⊥D1F;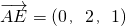 ,得
,得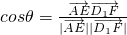 =
=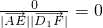
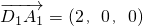 ,
,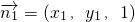 ,设平面A1FD1的法向量为
,设平面A1FD1的法向量为 ,
,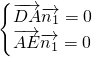
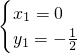
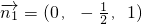

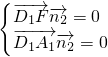
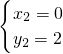
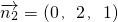
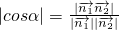 =
=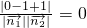
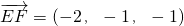 ,
,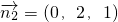
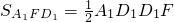 =
= ,
,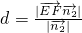 =
=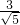 ,
,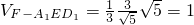 .
.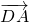
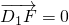 ,可证AD⊥D1F;
,可证AD⊥D1F;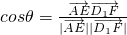 =
=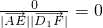 ,可求AE与D1F所成的角;(3)由题意:
,可求AE与D1F所成的角;(3)由题意: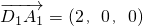 ,
,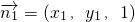 ,设平面A1FD1的法向量为
,设平面A1FD1的法向量为 ,证明平面的法向量垂直,即可证明面AED⊥面A1FD1.
,证明平面的法向量垂直,即可证明面AED⊥面A1FD1.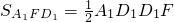 =
= ,计算E到平面A1FD1的距离
,计算E到平面A1FD1的距离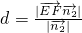 =
=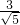 ,即可求三棱锥的体积.
,即可求三棱锥的体积.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则 若Rt△ABC中两直角边为a、b,斜边c上的高为h,则
若Rt△ABC中两直角边为a、b,斜边c上的高为h,则