
【题目】已知当x<1时,f(x)=(2﹣a)x+1;当x≥1时,f(x)=ax(a>0且a≠1).若对任意x1≠x2 , 都有 ![]() 成立,则a的取值范围是( )
成立,则a的取值范围是( )
A.(1,2)
B.![]()
C.![]()
D.(0,1)∪(2,+∞)
科目:高中数学 来源: 题型:
【题目】随着共享单车的成功运营,更多的共享产品逐步走入大家的世界,共享汽车、共享篮球、共享充电宝等各种共享产品层出不穷.某公司随即抽取![]() 人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的
人对共享产品是否对日常生活有益进行了问卷调查,并对参与调查的![]() 人中的性别以及意见进行了分类,得到的数据如下表所示:
人中的性别以及意见进行了分类,得到的数据如下表所示:
男 | 女 | 总计 | |
认为共享产品对生活有益 |
|
|
|
认为共享产品对生活无益 |
|
|
|
总计 |
|
|
|
(1)根据表中的数据,能否在犯错误的概率不超过![]() 的前提下,认为对共享产品的态度与性别有关系?
的前提下,认为对共享产品的态度与性别有关系?
(2)现按照分层抽样从认为共享产品增多对生活无益的人员中随机抽取![]() 人,再从
人,再从![]() 人中随机抽取
人中随机抽取![]() 人赠送超市购物券作为答谢,求恰有
人赠送超市购物券作为答谢,求恰有![]() 人是女性的概率.
人是女性的概率.
参与公式: 
临界值表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知集合A={y|y= ![]() },B={x|y=lg(x﹣2x2)},则R(A∩B)=( )
},B={x|y=lg(x﹣2x2)},则R(A∩B)=( )
A.[0, ![]() )
)
B.(﹣∞,0)∪[ ![]() ,+∞)
,+∞)
C.(0, ![]() )
)
D.(﹣∞,0]∪[ ![]() ,+∞)
,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义下凸函数如下:设f(x)为区间I上的函数,若对任意的x1 , x2∈I总有f( ![]() )≥
)≥ ![]() ,则称f(x)为I上的下凸函数,某同学查阅资料后发现了下凸函数有如下判定定理和性质定理: 判定定理:f(x)为下凸函数的充要条件是f″(x)≥0,x∈I,其中f″(x)为f(x)的导函数f′(x)的导数.
,则称f(x)为I上的下凸函数,某同学查阅资料后发现了下凸函数有如下判定定理和性质定理: 判定定理:f(x)为下凸函数的充要条件是f″(x)≥0,x∈I,其中f″(x)为f(x)的导函数f′(x)的导数.
性质定理:若函数f(x)为区间I上的下凸函数,则对I内任意的x1 , x2 , …,xn , 都有 ![]() ≥f(
≥f( ![]() ).
).
请问:在△ABC中,sinA+sinB+sinC的最大值为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=xlnx.
(Ⅰ)设函数g(x)= ![]() ,求g(x)的单调区间;
,求g(x)的单调区间;
(Ⅱ)若方程f(x)=t有两个不相等的实数根x1 , x2 , 求证:x1+x2 ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某气象站观测点记录的连续4天里,AQI指数M与当天的空气水平可见度y(单位cm)的情况如下表1:
M | 900 | 700 | 300 | 100 |
y | 0.5 | 3.5 | 6.5 | 9.5 |
哈尔滨市某月AQI指数频数分布如下表2:
M | [0,200] | (200,400] | (400,600] | (600,800] | (800,1000] |
频数 | 3 | 6 | 12 | 6 | 3 |
(1)设x= ![]() ,根据表1的数据,求出y关于x的回归方程; (参考公式:
,根据表1的数据,求出y关于x的回归方程; (参考公式: ![]() ;其中
;其中 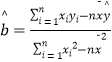 ,
, ![]() )
)
(2)小张开了一家洗车店,经统计,当M不高于200时,洗车店平均每天亏损约2000元;当M在200至400时,洗车店平均每天收入约4000元;当M大于400时,洗车店平均每天收入约7000元;根据表2估计小张的洗车店该月份平均每天的收入.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系中,以原点O为极点,x轴为正半轴为极轴,建立极坐标系.设曲线C: ![]() (α为参数);直线l:ρ(cosθ+sinθ)=4.
(α为参数);直线l:ρ(cosθ+sinθ)=4.
(Ⅰ)写出曲线C的普通方程和直线l的直角坐标方程;
(Ⅱ)求曲线C上的点到直线l的最大距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,AC是弦,∠BAC的平分线AD交圆O于点D,DE⊥AC,交AC的延长线于点E,OE交AD于点F. 
(1)求证:DE是圆O的切线;
(2)若∠CAB=60°,⊙O的半径为2,EC=1,求DE的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
在直角坐标系xOy中,直线l1的参数方程为 ![]() ,(t为参数),直线l2的参数方程为
,(t为参数),直线l2的参数方程为 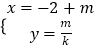 ,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(10分)
,(m为参数).设l1与l2的交点为P,当k变化时,P的轨迹为曲线C.(10分)
(1)写出C的普通方程;
(2)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,设l3:ρ(cosθ+sinθ)﹣ ![]() =0,M为l3与C的交点,求M的极径.
=0,M为l3与C的交点,求M的极径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com