
【题目】已知函数f(x)=xlnx.
(Ⅰ)设函数g(x)= ![]() ,求g(x)的单调区间;
,求g(x)的单调区间;
(Ⅱ)若方程f(x)=t有两个不相等的实数根x1 , x2 , 求证:x1+x2 ![]() .
.
【答案】解:(Ⅰ)∵g(x)= ![]() (x>0,且x≠1),则g′(x)=
(x>0,且x≠1),则g′(x)= ![]() (x>0,且x≠1), 设h(x)=x﹣lnx﹣1(x>0,且x≠1),则h′(x)=1﹣
(x>0,且x≠1), 设h(x)=x﹣lnx﹣1(x>0,且x≠1),则h′(x)=1﹣ ![]() (x>0,且x≠1),
(x>0,且x≠1),
当0<x<1时,h′(x)<0,h(x)单调递减;x>1时,h′(x)>0,h(x)单调递增;
∴h(x)>h(1)=0,
∴当x>0,且x≠1时,f′(x)>0,f(x)单调递增,
∴g(x)的单调递增区间(0,1),(1,+∞),无单调递增区间;
(Ⅱ)证明:f′(x)=1+lnx,当0<x< ![]() ,f′(x)>0,则f(x)在(0,
,f′(x)>0,则f(x)在(0, ![]() )单调递减,
)单调递减,
当x> ![]() 时,f′(x)>0,函数f(x)在(
时,f′(x)>0,函数f(x)在( ![]() ,+∞)上单调递增,
,+∞)上单调递增,
当0<x<1时,f(x)<0,当x>1,f(x)>0,
设0<x1< ![]() x2<1,构造函数F(x)=f(x)﹣f(x﹣
x2<1,构造函数F(x)=f(x)﹣f(x﹣ ![]() ),
),
则F′(x)=f′(x)﹣f′( ![]() ﹣x)=2+lnx(
﹣x)=2+lnx( ![]() ﹣x),
﹣x),
当0<x< ![]() ,x(
,x( ![]() ﹣x)<
﹣x)< ![]() ,则F′(x)<0,F(x)在(0,
,则F′(x)<0,F(x)在(0, ![]() )单调递减,
)单调递减,
由F( ![]() )=0,故F(x)>0,(0<e<
)=0,故F(x)>0,(0<e< ![]() ),
),
由0<x1< ![]() ,得F(x1)=f(x1)﹣f(
,得F(x1)=f(x1)﹣f( ![]() ﹣x1)>0,
﹣x1)>0,
则f(x1)=f(x2)>f( ![]() ﹣x1),
﹣x1),
又x2> ![]() ,
, ![]() ﹣x1>
﹣x1> ![]() ,
,
∴f(x)在( ![]() ,+∞)上单调递增,故x2>
,+∞)上单调递增,故x2> ![]() ﹣x1 ,
﹣x1 ,
∴x1+x2![]()
【解析】(Ⅰ)求导,根据函数的单调性导数的关系,构造辅助函数,求导h′(x)=1﹣ ![]() (x>0,且x≠1),则h(x)>h(1)=0,则f′(x)>0,即可求得g(x)的单调区间;(Ⅱ)构造函数F(x)=f(x)﹣f(x﹣
(x>0,且x≠1),则h(x)>h(1)=0,则f′(x)>0,即可求得g(x)的单调区间;(Ⅱ)构造函数F(x)=f(x)﹣f(x﹣ ![]() ),求导F′(x)=2+lnx(
),求导F′(x)=2+lnx( ![]() ﹣x),根据函数单调性可知F(x)>0,(0<e<
﹣x),根据函数单调性可知F(x)>0,(0<e< ![]() ),当0<x1<
),当0<x1< ![]() ,得F(x1)=f(x1)﹣f(
,得F(x1)=f(x1)﹣f( ![]() ﹣x1)>0,f(x)在(
﹣x1)>0,f(x)在( ![]() ,+∞)上单调递增,故x2>
,+∞)上单调递增,故x2> ![]() ﹣x1 , 即可求证不等式成立.
﹣x1 , 即可求证不等式成立.
【考点精析】解答此题的关键在于理解利用导数研究函数的单调性的相关知识,掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数
在这个区间单调递减,以及对函数的最大(小)值与导数的理解,了解求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值.
比较,其中最大的是一个最大值,最小的是最小值.


科目:高中数学 来源: 题型:
【题目】现在,很多人都喜欢骑“共享单车”,但也有很多市民并不认可.为了调查人们对这种交通方式的认可度,某同学从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20名市民,得到了一个市民是否认可的样本,具体数据如下![]() 列联表:
列联表:
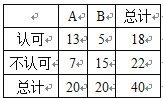
附:![]() ,
,![]() .
.

根据表中的数据,下列说法中,正确的是( )
A. 没有95% 以上的把握认为“是否认可与城市的拥堵情况有关”
B. 有99% 以上的把握认为“是否认可与城市的拥堵情况有关”
C. 可以在犯错误的概率不超过0.01的前提下认为“是否认可与城市的拥堵情况有关”
D. 可以在犯错误的概率不超过0.025的前提下认为“是否认可与城市的拥堵情况有关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥P﹣ABC中,AP=AB,平面PAB⊥平面ABC,∠ABC=90°,D,E分别为PB,BC的中点.
(1)求证:DE∥平面PAC;
(2)求证:DE⊥AD.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】十九大提出,坚决打赢脱贫攻坚战,某帮扶单位为帮助定点扶贫村真脱贫,坚持扶贫同扶智相结合,帮助贫困村种植蜜柚,并利用电商进行销售,为了更好地销售,现从该村的蜜柚树上随机摘下了100个蜜柚进行测重,其质量分别在![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (单位:克)中,其频率分布直方图如图所示.
(单位:克)中,其频率分布直方图如图所示.

(1)求质量落在![]() ,
, ![]() 两组内的蜜柚的抽取个数,
两组内的蜜柚的抽取个数,
(2)从质量落在![]() ,
, ![]() 内的蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
内的蜜柚中随机抽取2个,求这2个蜜柚质量均小于2000克的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2016年美国总统大选过后,有媒体从某公司的全体员工中随机抽取了200人,对他们的投票结果进行了统计(不考虑弃权等其他情况),发现支持希拉里的一共有95人,其中女员工55人,支持特朗普的男员工有60人.
(Ⅰ)根据已知条件完成下面的2×2列联表:据此材料,是否有95%的把握认为投票结果与性别有关?
支持希拉里 | 支持特朗普 | 合计 | |
男员工 | |||
女员工 | |||
合计 |
(Ⅱ)若从该公司的所有男员工中随机抽取3人,记其中支持特朗普的人数为X,求随机变量X的分布列和数学期望.(用相应的频率估计概率)
附:
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式:K2= ![]() ,其中n=a+b+c+d)
,其中n=a+b+c+d)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知当x<1时,f(x)=(2﹣a)x+1;当x≥1时,f(x)=ax(a>0且a≠1).若对任意x1≠x2 , 都有 ![]() 成立,则a的取值范围是( )
成立,则a的取值范围是( )
A.(1,2)
B.![]()
C.![]()
D.(0,1)∪(2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的奇函数f(x)满足f(x)=x2﹣2x﹣3(x>0).
(Ⅰ) 若函数g(x)=|f(x)|﹣a有4个零点,求实数a的取值范围;
(Ⅱ) 求|f(x+1)|≤4的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设p:实数x满足x2﹣4ax+3a2<0,q:实数x满足|x﹣3|<1.
(1)若a=1,且p∧q为真,求实数x的取值范围;
(2)若其中a>0且¬p是¬q的充分不必要条件,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com