
【题目】已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(Ⅰ)求![]() 的值;
的值;
(Ⅱ)求证: ![]()
![]() .
.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】
(I)![]() .可得a1=S1=1﹣1=0,a1+a2=22+1,a1+a2+a3=32﹣1,联立解
.可得a1=S1=1﹣1=0,a1+a2=22+1,a1+a2+a3=32﹣1,联立解
得a1,a2,a3.(II)n≥2时,an=Sn﹣Sn﹣1=2n﹣1+2(﹣1)n.当n为偶数时,an=2n+1;
当n为奇数时,an=2n﹣3(n>1).利用等差数列的求和公式即可得出.
(I)解:∵![]() .∴a1=S1=1﹣1=0,a1+a2=22+1,a1+a2+a3=32﹣1,
.∴a1=S1=1﹣1=0,a1+a2=22+1,a1+a2+a3=32﹣1,
联立解得:a1=0,a2=5,a3=3.
(II)证明:n≥2时,an=Sn﹣Sn﹣1=n2+(﹣1)n﹣[(n﹣1)2+(﹣1)n﹣1]
=2n﹣1+2(﹣1)n.
当n为偶数时,an=2n+1;当n为奇数时,an=2n﹣3(n>1).
∴a1+a3+a5+…+a2n+1=0+3+7+……+2(2n+1)﹣3=![]() =2n2+n.
=2n2+n.
a2+a4+a6+…+a2n=5+9+……+(2n+1)=![]() =2n2+3n.
=2n2+3n.
∵2n2+3n﹣(2n2+n)=2n>0.
∴a1+a3+a5+…+a2n+1<a2+a4+a6+…+a2n.


科目:高中数学 来源: 题型:
【题目】如图,已知椭圆![]() 的左顶点为
的左顶点为![]() ,过右焦点
,过右焦点![]() 的直线交椭圆于
的直线交椭圆于![]() ,
,![]() 两点,直线
两点,直线![]() ,
,![]() 分别交直线
分别交直线![]() 于点
于点![]() ,
,![]() .
.

(1)试判断以线段![]() 为直径的圆是否过点
为直径的圆是否过点![]() ,并说明理由;
,并说明理由;
(2)记![]() ,
,![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,
,![]() ,证明:
,证明:![]() ,
,![]() ,
,![]() 成等差数列.
成等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形![]() 所在平面与直角梯形
所在平面与直角梯形![]() 所在平面互相垂直,且
所在平面互相垂直,且![]() ,
,![]() 为
为![]() 中点.
中点.
(1)求异面直线![]() 与
与![]() 所成的角;
所成的角;
(2)求平面![]() 与平面
与平面![]() 所成的二面角(锐角)的余弦值.
所成的二面角(锐角)的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() +1(
+1(![]() )在(0,+∞)内有且只有一个零点,则
)在(0,+∞)内有且只有一个零点,则![]() 在[﹣1,1]上的值域为
在[﹣1,1]上的值域为
A. [﹣4,0] B. [﹣4,1] C. [﹣1,3] D. [﹣![]() ,12]
,12]
查看答案和解析>>
科目:高中数学 来源: 题型:
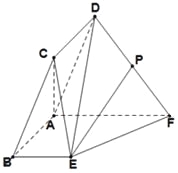
【题目】如图,在底面是菱形的四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,点
,点![]() 分别为
分别为![]() 的中点,设直线
的中点,设直线![]() 与平面
与平面![]() 交于点
交于点![]() .
.

(1)已知平面![]() 平面
平面![]() ,求证:
,求证: ![]() .
.
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com