
分析 (1)由已知得a=2c,且$∠{F_1}M{F_2}={60^0}$,由余弦定理求出c=1.由此能求出椭圆C的方程.
(2)设直线l的方程为y=kx+(1-4k),代入椭圆方程,得(3+4k2)x2+(8k-32k2)x+64k2-32k-8=0,由此利用韦达定理、向量,结合已知条件能证明点Q总在某定直线上,并求出该定直线.
解答 解:(1)∵椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的离心率为$\frac{1}{2}$,
左、右焦点分别为圆F1、F2,M是C上一点,|MF1|=2,且$|{\overrightarrow{M{F_1}}}||{\overrightarrow{M{F_2}}}|=-2\overrightarrow{M{F_1}}•\overrightarrow{{F_2}M}$.
∴由已知得a=2c,且$∠{F_1}M{F_2}={60^0}$,
在△F1F2M中,由余弦定理得:
(2c)2=22+(4c-2)2-2×2(4c-2)cos60°,
解得c=1.则$a=2,b=\sqrt{3}$,
所以椭圆C的方程为$\frac{x^2}{4}+\frac{y^2}{3}=1$.
证明:(2)由题意可得直线l的斜率存在,
设直线l的方程为y-1=k(x-4),即y=kx+(1-4k),
代入椭圆方程,整理得(3+4k2)x2+(8k-32k2)x+64k2-32k-8=0,
设A(x1,y1),B(x2,y2),
则${x_1}+{x_2}=\frac{{32{k^2}-8k}}{{3+4{k^2}}},{x_1}{x_2}=\frac{{64{k^2}-32k-8}}{{3+4{k^2}}}$.
设Q(x0,y0),由$|{\overrightarrow{AP}}||{\overrightarrow{QB}}|=|{\overrightarrow{AQ}}||{\overrightarrow{PB}}|$,得:
(4-x1)(x0-x2)=(x1-x0)(4-x2)(考虑线段在x轴上的射影即可),
∴8x0=(4+x0)(x1+x2)-2x1x2,
于是$8{x_0}=({4+{x_0}})\frac{{32{k^2}-8k}}{{3+4{k^2}}}-2×\frac{{64{k^2}-32k-8}}{{3+4{k^2}}}$,
整理得3x0-2=(4-x0)k,(*)
又$k=\frac{{{y_0}-1}}{{{x_0}-4}}$,代入(*)式得3x0+y0-3=0,
∴点Q总在直线3x+y-3=0上.
点评 本题考查椭圆方程的求法,考查点总在定直线上的证明,考查直线方程的求法,考查椭圆、直线方程、向量、韦达定理等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想,是中档题.


科目:高中数学 来源: 题型:解答题
| 选择套餐种类 | A | B | C |
| 选择每种套餐的人数 | 50 | 25 | 25 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $-\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
| 八卦 |  |  | 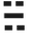 | 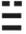 | … |  | … |
| 二进制 | 000 | 001 | 010 | 011 | … | A | … |
| 十进制 | 0 | 1 | 2 | 3 | … | B | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
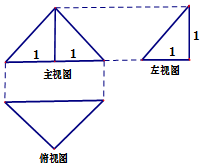
| A. | $\frac{4}{3}π$ | B. | $\frac{{\sqrt{3}}}{2}π$ | C. | $\frac{{5\sqrt{5}}}{6}π$ | D. | $\sqrt{6}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1+$\frac{1}{2}$<2 | B. | 1+$\frac{1}{2}$+$\frac{1}{3}$<3 | C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$<3 | D. | 1+$\frac{1}{2}$+$\frac{1}{3}$<2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com