
在△ABC中,角A,B,C的对边分别为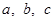 ,且A,B,C成等差数列。
,且A,B,C成等差数列。
(1)若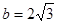 ,
,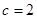 ,求△ABC的面积;
,求△ABC的面积;
(2)若 成等比数列,试判断△ABC的形状。
成等比数列,试判断△ABC的形状。
(1) ;(2)等边三角形
;(2)等边三角形
解析试题分析:(1)由A,B,C成等差数列得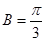 , 又
, 又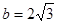 ,
,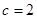 ,法一:由正弦定理得
,法一:由正弦定理得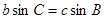 ,所以
,所以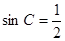 , 又
, 又 ,所以
,所以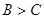 ,即C为锐角,所以
,即C为锐角,所以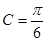 ,从而
,从而 , 所以
, 所以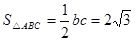 .法二:由余弦定理得
.法二:由余弦定理得 ,即
,即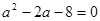 ,得
,得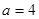 .所以
.所以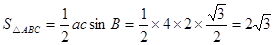
(2)由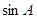 ,
,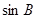 ,
, 成等比数列,所以
成等比数列,所以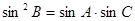 ,由正弦定理得
,由正弦定理得 由余弦定理得
由余弦定理得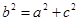
 , 所以
, 所以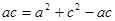 ,即
,即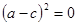 ,即
,即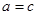 . 又因为
. 又因为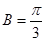 ,所以△ABC为等边三角形。
,所以△ABC为等边三角形。
试题解析:因为A,B,C成等差数列,所以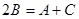 。又A+B+C=
。又A+B+C= ,所以
,所以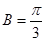 。
。
(1)解法一:因为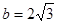 ,
,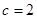 ,所以
,所以
由正弦定理得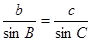 ,即
,即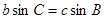 ,即
,即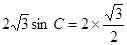 ,
,
得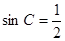 。
。
因为 ,所以
,所以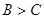 ,即C为锐角,所以
,即C为锐角,所以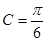 ,从而
,从而 。
。
所以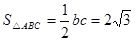 。
。
解法二:由余弦定理得 ,
,
即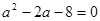 ,得
,得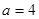 。
。
所以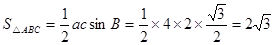 。
。
(2)因为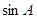 ,
,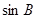 ,
, 成等比数列,所以
成等比数列,所以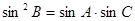 。
。
由正弦定理得
由余弦定理得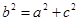
 。
。
所以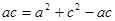 ,即
,即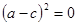 ,即
,即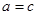 。
。
又因为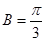 ,所以△ABC为等边三角形。
,所以△ABC为等边三角形。
考点:正弦定理与余弦定理以及等差、等比数列的性质


 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:解答题
如图,山顶有一座石塔 ,已知石塔的高度为
,已知石塔的高度为 .
.
(1)若以 为观测点,在塔顶
为观测点,在塔顶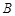 处测得地面上一点
处测得地面上一点 的俯角为
的俯角为 ,在塔底
,在塔底 处测得
处测得 处的俯角为
处的俯角为 ,用
,用 表示山的高度
表示山的高度 ;
;
(2)若将观测点选在地面的直线 上,其中
上,其中 是塔顶
是塔顶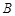 在地面上的射影. 已知石塔高度
在地面上的射影. 已知石塔高度 ,当观测点
,当观测点 在
在 上满足
上满足 时看
时看 的视角(即
的视角(即 )最大,求山的高度
)最大,求山的高度 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com