
| A. | 5-π | B. | 1+π | C. | π-3 | D. | 1-π |
分析 首先画出图形,利用定积分表示封闭图形的面积,然后计算即可.
解答 解: 函数f(x)=$\left\{\begin{array}{l}{\sqrt{4-{x}^{2}}-2,(-2≤x<0)}\\{|{x}^{2}-x|,(x≤x≤2)}\end{array}\right.$的图象与x轴及x=±2所围成的封闭图形如图,
函数f(x)=$\left\{\begin{array}{l}{\sqrt{4-{x}^{2}}-2,(-2≤x<0)}\\{|{x}^{2}-x|,(x≤x≤2)}\end{array}\right.$的图象与x轴及x=±2所围成的封闭图形如图,
其面积S=${∫}_{-2}^{0}(\sqrt{4-{x}^{2}}-2)dx{+∫}_{0}^{1}(x-{x}^{2})dx{+∫}_{1}^{2}({x}^{2}-x)dx\\;\\;\$
=$4-\frac{1}{4}π•{2}^{2}+(\frac{1}{2}{x}^{2}-\frac{1}{3}{x}^{3}){|}_{0}^{1}+(\frac{1}{3}{x}^{3}-\frac{1}{2}{x}^{2}){|}_{1}^{2}\\;=5-π\\;\\;\\;\$
=5-π.
故选:A.
点评 本题考查了利用定积分求曲边梯形的面积;关键是利用定积分表示出封闭图形的面积,然后计算.


科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 6 | C. | 8 | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
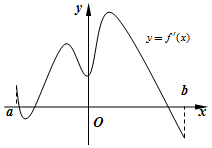 函数f(x)的定义域为开区间(a,b),其导函数f'(x)在(a,b)图象如图所示,则函数f(x)在开区间(a,b)内的极小值的个数是1个.
函数f(x)的定义域为开区间(a,b),其导函数f'(x)在(a,b)图象如图所示,则函数f(x)在开区间(a,b)内的极小值的个数是1个.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${(\frac{sinx}{x})^2}<\frac{{sin{x^2}}}{x^2}<\frac{sinx}{x}$ | B. | $\frac{{sin{x^2}}}{x^2}<\frac{sinx}{x}<{(\frac{sinx}{x})^2}$ | ||
| C. | ${(\frac{sinx}{x})^2}<\frac{sinx}{x}<\frac{{sin{x^2}}}{x^2}$ | D. | $\frac{sinx}{x}<\frac{{sin{x^2}}}{x^2}<{(\frac{sinx}{x})^2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | $\sqrt{3}$ | C. | $\frac{3}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5.2 | B. | 6.6 | C. | 7.1 | D. | 8.3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com