
【题目】已知椭圆![]() 的中心在原点,焦点在
的中心在原点,焦点在![]() 轴上,离心率为
轴上,离心率为![]() ,它的一个顶点恰好是抛物线
,它的一个顶点恰好是抛物线![]() 的焦点.
的焦点.

(1)求椭圆![]() 的方程;
的方程;
(2)直线![]() 与椭圆交于
与椭圆交于![]() 两点,
两点,![]() 点位于第一象限,
点位于第一象限,![]() 是椭圆上位于直线
是椭圆上位于直线![]() 两侧的动点.
两侧的动点.
(i)若直线![]() 的斜率为
的斜率为![]() ,求四边形
,求四边形![]() 面积的最大值;
面积的最大值;
(ii)当点![]() 运动时,满足
运动时,满足![]() ,问直线
,问直线![]() 的斜率是否为定值,请说明理由.
的斜率是否为定值,请说明理由.
【答案】(I)![]() ;(Ⅱ)(i)
;(Ⅱ)(i)![]() ;(ii)
;(ii)![]() 的斜率为定值
的斜率为定值![]() .
.
【解析】
试题(I)设椭圆![]() 的方程为
的方程为![]() ,由条件利用椭圆的性质求得
,由条件利用椭圆的性质求得![]() 和
和![]() 的值,可得椭圆
的值,可得椭圆![]() 的方程.
的方程.
(II)(i)设![]() 的方程为
的方程为![]() ,代入椭圆
,代入椭圆![]() 的方程化简,由△>0,求得
的方程化简,由△>0,求得![]() 的范围,再利用利用韦达定理可得
的范围,再利用利用韦达定理可得![]() 以及
以及![]() 的值.再求得
的值.再求得![]() 的坐标,根据四边形
的坐标,根据四边形![]() 的面积
的面积![]() ,计算求得结果.
,计算求得结果.
(ii)当![]() 时,C、
时,C、![]() 的斜率之和等于零,
的斜率之和等于零,![]() 的方程为
的方程为![]() ,把它代入椭圆
,把它代入椭圆![]() 的方程化简求得
的方程化简求得![]() .再把直线
.再把直线![]() 的方程椭圆
的方程椭圆![]() 的方程化简求得
的方程化简求得![]() 的值,可得
的值,可得![]() 以及
以及![]() 的值,从而求得
的值,从而求得![]() 的斜率
的斜率![]() 的值.
的值.
试题解析:设椭圆![]() 的方程为
的方程为![]() ,由题意可得它的一个顶点恰好是抛物线
,由题意可得它的一个顶点恰好是抛物线![]() 的焦点
的焦点![]() ,
,![]() .
.
再根据离心率![]() ,求得
,求得![]() ,∴椭圆C的方程为
,∴椭圆C的方程为![]() .
.
(Ⅱ)(i)设![]() ,
,![]() 的方程为
的方程为![]() ,代入椭圆
,代入椭圆![]() 的方程化简可得
的方程化简可得![]() ,由
,由![]() ,求得
,求得![]() .
.
利用韦达定理可得![]() ,
,![]() .
.
在![]() 中,令
中,令![]() 求得
求得![]() ,∴四边形
,∴四边形![]() 的面积
的面积
![]()
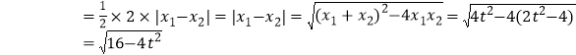 ,
,
故当![]() 时,四边形
时,四边形![]() 的面积
的面积![]() 取得最小值为4.
取得最小值为4.
(ii)当![]() 时,
时,![]() 、
、![]() 的斜率之和等于零,设
的斜率之和等于零,设![]() 的斜率为
的斜率为![]() ,则
,则![]() 的斜率为
的斜率为![]() ,
,
![]() 的方程为
的方程为![]() ,把它代入椭圆
,把它代入椭圆![]() 的方程化简可得
的方程化简可得
![]() ,所以
,所以![]() .
.
同理可得直线![]() 的方程为
的方程为![]() ,
,
![]() ,
,
![]() 的斜率
的斜率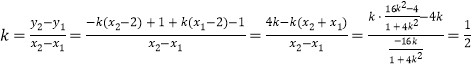 .
.


 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案科目:高中数学 来源: 题型:
【题目】《九章算术》中“竹九节”问题:现有一根9节的竹子,自上而下各节的容积成等差数列,上面4节的容积共3升,下面3节的容积共4升,则第6节的容积为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点A(﹣2,0),B(0,1)在椭圆C: ![]() (a>b>0)上.
(a>b>0)上.
(Ⅰ)求椭圆C的方程;
(Ⅱ)P是线段AB上的点,直线y= ![]() x+m(m≥0)交椭圆C于M、N两点,若△MNP是斜边长为
x+m(m≥0)交椭圆C于M、N两点,若△MNP是斜边长为 ![]() 的直角三角形,求直线MN的方程.
的直角三角形,求直线MN的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在锐角△ABC中,a、b、c分别是角A、B、C的对边,若A满足2cos2A+cos(2A+ ![]() )=﹣
)=﹣ ![]() .
.
(Ⅰ)求A的值;
(Ⅱ)若c=3,△ABC的面积为3 ![]() ,求a的值.
,求a的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义在R上的函数y=f(x)为减函数,且函数y=f(x﹣1)的图象关于点(1,0)对称,若f(x2﹣2x)+f(2b﹣b2)≤0,且0≤x≤2,则x﹣b的取值范围是( )
A.[﹣2,0]
B.[﹣2,2]
C.[0,2]
D.[0,4]
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校某文具商店经营某种文具,商店每销售一件该文具可获利3元,若供大于求则削价处理,每处理一件文具亏损1元;若供不应求,则可以从外部调剂供应,此时每件文具仅获利2元.为了了解市场需求的情况,经销商统计了去年一年(52周)的销售情况.
销售量(件) | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
周数 | 2 | 4 | 8 | 13 | 13 | 8 | 4 |
以去年每周的销售量的频率为今年每周市场需求量的概率.
(1)要使进货量不超过市场需求量的概率大于0.5,问进货量的最大值是多少?
(2)如果今年的周进货量为14,写出周利润Y的分布列;
(3)如果以周利润的期望值为考虑问题的依据,今年的周进货量定为多少合适?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() ,离心率为
,离心率为![]() ,并过点
,并过点![]() .
.
(1)求椭圆方程;
(2)若直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点(
两点(![]() 不是左右顶点),且以
不是左右顶点),且以![]() 为直径的圆过椭圆
为直径的圆过椭圆![]() 的右顶点。求证:直线
的右顶点。求证:直线![]() 过定点,并求出该定点的坐标.
过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义![]() 为n个正数
为n个正数![]() 的“均倒数”.已知正项数列{an}的前n项的“均倒数”为
的“均倒数”.已知正项数列{an}的前n项的“均倒数”为![]() .
.
(1)求数列{an}的通项公式.
(2)设数列![]() 的前n项和为
的前n项和为![]() ,若4
,若4![]() <
<![]() 对一切
对一切![]() 恒成立试求实数m的取值范围.
恒成立试求实数m的取值范围.
(3)令![]() ,问:是否存在正整数k使得
,问:是否存在正整数k使得![]() 对一切
对一切![]() 恒成立,如存在求出k值,否则说明理由.
恒成立,如存在求出k值,否则说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com