练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)=lg(a x2+2x+1)

    （1）若f(x)的定义域是R，求实数a的取值范围及f(x)的值域；

    （2）若f(x)的值域是R，求实数a的取值范围及f(x)的定义域.

    解析：（1）因为f(x)的定义域为R，所以ax2+2x+1>0对一切xR成立．

    由此得解得a>1.    又因为ax2+2x+1=a(x+)+1－>0，

    所以f(x)=lg(a x2+2x+1) lg(1－)，所以实数a的取值范围是(1,+ ) ,

    f(x)的值域是

    ( 2 ) 因为f(x)的值域是R，所以u=ax2+2x+1的值域(0, +).

    当a=0时，u=2x+1的值域为R(0, +)；

    当a≠0时，u=ax2+2x+1的值域(0, +)等价于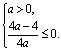

    解之得0<a1.  所以实数a的取值范围是[0.1]    当a=0时，由2x+1>0得x>－,

    f (x)的定义域是(－,+)；  当0<a1时，由ax2+2x+1>0

    解得  

    f (x)的定义域是
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    1
    3
    x3-
    3
    2
    ax2-(a-3)x+b
    （1）若函数f（x）在P（0，f（0））的切线方程为y=5x+1，求实数a，b的值：
    （2）当a＜3时，令g(x)=
    f′(x)
    x
    ，求y=g（x）在[l，2]上的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    1
    2
    x2-alnx    的图象在点P（2，f（2））处的切线方程为l：y=x+b
    （1）求出函数y=f（x）的表达式和切线l的方程；
    （2）当x∈[
    1
    e
    ，e]    时（其中e=2.71828…），不等式f（x）＜k恒成立，求实数k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=lnx，g(x)=
    12
    x2+a    （a为常数），直线l与函数f（x）、g（x）的图象都相切，且l与函数f（x）的图象的切点的横坐标为1．
    （1）求直线l的方程及a的值；
    （2）当k＞0时，试讨论方程f（1+x2）-g（x）=k的解的个数．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=
    13
    x3+x2+ax    ．
    （1）讨论f（x）的单调性；
    （2）设f（x）有两个极值点x1，x2，若过两点（x1，f（x1）），（x2，f（x2））的直线l与x轴的交点在曲线y=f（x）上，求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)=x3-
    32
    ax2+b    ，a，b为实数，x∈R，a∈R．
    （1）当1＜a＜2时，若f（x）在区间[-1，1]上的最小值、最大值分别为-2、1，求a、b的值；
    （2）在（1）的条件下，求经过点P（2，1）且与曲线f（x）相切的直线l的方程；
    （3）试讨论函数F（x）=（f′（x）-2x2+4ax+a+1）•ex的极值点的个数．

    查看答案和解析>>

    同步练习册答案