
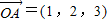 ,
,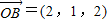 ,
,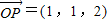 ,点Q在直线OP上运动,则当
,点Q在直线OP上运动,则当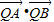 取得最小值时,点Q的坐标为 .
取得最小值时,点Q的坐标为 . 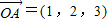 ,
,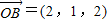 ,
,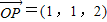 ,点Q在直线OP上运动,我们可以设
,点Q在直线OP上运动,我们可以设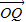 =λ
=λ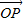 =(λ,λ,2λ),求出向量
=(λ,λ,2λ),求出向量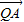 ,
,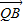 的坐标,代入空间向量的数量积运算公式,再根据二次函数的性质,可得到满足条件的λ的值,进而得到点Q的坐标.
的坐标,代入空间向量的数量积运算公式,再根据二次函数的性质,可得到满足条件的λ的值,进而得到点Q的坐标.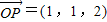 ,点Q在直线OP上运动,
,点Q在直线OP上运动,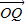 =λ
=λ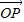 =(λ,λ,2λ)
=(λ,λ,2λ)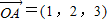 ,
,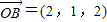 ,
,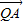 =(1-λ,2-λ,3-2λ),
=(1-λ,2-λ,3-2λ),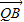 =(2-λ,1-λ,2-2λ)
=(2-λ,1-λ,2-2λ)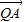 •
•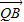 =(1-λ)×(2-λ)+(2-λ)×(1-λ)+(3-2λ)×(2-2λ)=6λ2-16λ+10
=(1-λ)×(2-λ)+(2-λ)×(1-λ)+(3-2λ)×(2-2λ)=6λ2-16λ+10 时,
时,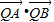 取得最小值.
取得最小值.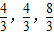 )
)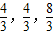 )
)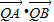 的表达式,进而将问题转化为一个二次函数最值问题,是解答本题的关键.
的表达式,进而将问题转化为一个二次函数最值问题,是解答本题的关键. 

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:
| OA |
| OB |
| OP |
| QA |
| QB |
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| OP |
| QA |
| QB |
查看答案和解析>>
科目:高中数学 来源: 题型:
(06年江西卷理)设O为坐标原点,F为抛物线y2=4x的焦点,A是抛物线上一点,若![]() =-4则点A的坐标是( )
=-4则点A的坐标是( )
A.(2,±2![]() ) B. (1,±2) C.(1,2)D.(2,2
) B. (1,±2) C.(1,2)D.(2,2![]() )
)
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
| OA |
| OB |
| OP |
| QA |
| QB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com