
(本题满分12分)
已知函数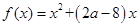 ,不等式
,不等式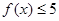 的解集是
的解集是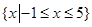 .
.
(1)求实数 的值;
的值;
(2) 对于
对于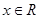 恒成立,求实数
恒成立,求实数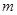 的取值范围.
的取值范围.
(1) ;
;
(2) 的单调递增区间是
的单调递增区间是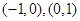 ,单调递减区间是
,单调递减区间是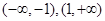 .(12分)
.(12分)
解析试题分析:(1)根据二次函数的不等式的解集,结合韦达定理可知参数a,b的值,求解解析式。
(2)要使得不等式 对于
对于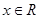 恒成立,,只要求解函数f(x)的最小值即可。转化与划归思想的运用。
恒成立,,只要求解函数f(x)的最小值即可。转化与划归思想的运用。
解(1)设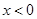 ,则
,则 ,
,
所以 (3分)
(3分)
又 是
是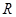 上的奇函数,则
上的奇函数,则 ,
, (4分)
(4分)
所以, (6分)
(6分)
(2)函数 的图像略
的图像略
(画图像关键点必须画准确,如顶点、端点、点的虚实,变化趋势等9分)
根据函数 的图像可知,
的图像可知, 的单调递增区间是
的单调递增区间是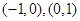 ,
,
单调递减区间是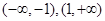 .(12分)
.(12分)
考点:本题主要考查了一元二次不等式的应用,二次函数性质的运用。体现了分类讨论的数学思想.
点评:解决该试题的关键是能结合不等式的解集得到参数的取值进而得到解析式,而对于恒成立的问题,通常转化为最大值或者最小值问题来处理即可。


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:高中数学 来源: 题型:解答题
某城市1995年底人口为500万,人均住房面积为6 m2,如果该城市每年人口平均增长率为1%,则从1996年起,政府为解决民生推动经济适用房建设,每年平均需新增住房面积为多少万m2,才能使2014年底该城市人均住房面积至少为24m2?(可参考的数据1.0118=1.20,1.0119=1.21,1.0120="1.22)."
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com