
【题目】设![]() 为常数,函数
为常数,函数![]() ,给出以下结论:
,给出以下结论:
(1)若![]() ,则
,则![]() 存在唯一零点
存在唯一零点
(2)若![]() ,则
,则![]()
(3)若![]() 有两个极值点
有两个极值点![]() ,则
,则![]()
其中正确结论的个数是( )
A. 3B. 2C. 1D. 0
【答案】A
【解析】
(1)先根据函数![]() 存在零点,得到方程
存在零点,得到方程![]() 有实根,再令
有实根,再令![]() ,将问题转为函数
,将问题转为函数![]() 图像与直线
图像与直线![]() 有交点即可,用导数的方法研究函数
有交点即可,用导数的方法研究函数![]() 单调性和最值,即可得出结论成立;
单调性和最值,即可得出结论成立;
(2)根据(1)的结果,可判断当![]() 时,
时,![]() 在
在![]() 上恒成立,从而可得
上恒成立,从而可得![]() 在
在![]() 上恒成立,即可得出结论成立;
上恒成立,即可得出结论成立;
(3)先对函数![]() 求导,根据题意得到
求导,根据题意得到![]() ,再将函数
,再将函数![]() 有两极值点,转化为方程
有两极值点,转化为方程![]() 有两不等式实根来处理,用导数的方法研究其单调性,和值域,进而可得出结论成立.
有两不等式实根来处理,用导数的方法研究其单调性,和值域,进而可得出结论成立.
(1)若函数![]() 存在零点,只需方程
存在零点,只需方程![]() 有实根,即方程
有实根,即方程![]() 有实根,令
有实根,令![]() ,则只需函数
,则只需函数![]() 图像与直线
图像与直线![]() 有交点即可.
有交点即可.
又![]() ,由
,由![]() 可得
可得![]() ;由
;由![]() 可得
可得![]() ;
;
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
故![]() ,
,
因此,当![]() 时,直线
时,直线![]() 与
与![]() 图像仅有一个交点,即原函数只有一个零点,所以(1)正确;
图像仅有一个交点,即原函数只有一个零点,所以(1)正确;
(2)由(1)可知,当![]() 时,
时,![]() 在
在![]() 上恒成立,
上恒成立,
即![]() 在
在![]() 上恒成立,即
上恒成立,即![]() 在
在![]() 上恒成立;故(2)正确;
上恒成立;故(2)正确;
(3)因为![]() ,所以
,所以![]() ,
,
若![]() 有两个极值点
有两个极值点![]() ,则
,则![]() ,所以
,所以![]() ,
,
又由![]() 有两个极值点,可得方程
有两个极值点,可得方程![]() 有两不等实根,即方程
有两不等实根,即方程![]() 有两不等式实根,令
有两不等式实根,令![]() ,则
,则![]() ,
,
由![]() 得
得![]() ;由
;由![]() 得
得![]() ;
;
所以函数![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减,
上单调递减,
所以![]() ,又当
,又当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;
;
所以方程![]() 有两不等式实根,只需直线
有两不等式实根,只需直线![]() 与函数
与函数![]() 的图像有两不同交点,故
的图像有两不同交点,故![]() ;所以
;所以![]() ,即(3)正确.
,即(3)正确.
故选A


科目:高中数学 来源: 题型:
【题目】某校研究性学习小组从汽车市场上随机抽取![]() 辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于
辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于![]() 公里和
公里和![]() 公里之间,将统计结果分成
公里之间,将统计结果分成![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,绘制成如图所示的频率分布直方图.
,绘制成如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)求续驶里程在![]() 的车辆数;
的车辆数;
(3)若从续驶里程在![]() 的车辆中随机抽取
的车辆中随机抽取![]() 辆车,求其中恰有一辆车的续驶里程在
辆车,求其中恰有一辆车的续驶里程在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司想了解对某产品投入的宣传费用与该产品的营业额的影响.右图是以往公司对该产品的宣传费用![]() (单位:万元)和产品营业额
(单位:万元)和产品营业额![]() (单位:万元)的统计折线图.
(单位:万元)的统计折线图.

(Ⅰ)根据折线图可以判断,可用线性回归模型拟合宣传费用![]() 与产品营业额
与产品营业额![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(Ⅱ)建立产品营业额![]() 关于宣传费用
关于宣传费用![]() 的回归方程;
的回归方程;
(Ⅲ)若某段时间内产品利润![]() 与宣传费
与宣传费![]() 和营业额
和营业额![]() 的关系为
的关系为![]() 应投入宣传费多少万元才能使利润最大,并求最大利润. (计算结果保留两位小数)
应投入宣传费多少万元才能使利润最大,并求最大利润. (计算结果保留两位小数)
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:相关系数 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘法估计公式分别为
中斜率和截距的最小二乘法估计公式分别为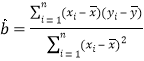 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,已知![]() 为椭圆
为椭圆![]() 的左焦点,且椭圆
的左焦点,且椭圆![]() 过
过![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ) 是否存在平行四边形 ![]() ,同时满足下列两个条件:
,同时满足下列两个条件:
①点![]() 在直线
在直线![]() 上;②点
上;②点 ![]() 在椭圆
在椭圆![]() 上且直线
上且直线 ![]() 的斜率等于1.如果存在,求出
的斜率等于1.如果存在,求出![]() 点坐标;如果不存在,说明理由.
点坐标;如果不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从一堆产品![]() 正品与次品都多于2件
正品与次品都多于2件![]() 中任取2件,观察正品件数和次品件数,则下列说法:
中任取2件,观察正品件数和次品件数,则下列说法:
![]() “恰好有1件次品”和“恰好2件都是次品”是互斥事件
“恰好有1件次品”和“恰好2件都是次品”是互斥事件
![]() “至少有1件正品”和“全是次品”是对立事件
“至少有1件正品”和“全是次品”是对立事件
![]() “至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件
“至少有1件正品”和“至少有1件次品”是互斥事件但不是对立事件
![]() “至少有1件次品”和“全是正品”是互斥事件也是对立事件
“至少有1件次品”和“全是正品”是互斥事件也是对立事件
其中正确的有______![]() 填序号
填序号![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据以往的经验,某建筑工程施工期间的降水量![]() (单位:
(单位:![]() )对工期的影响如下表:
)对工期的影响如下表:
降水量 |
|
|
|
|
工期延误天数 | 0 | 1 | 3 | 6 |
根据某气象站的资料,某调查小组抄录了该工程施工地某月前![]() 天的降水量的数据,绘制得到降水量的折线图,如下图所示.
天的降水量的数据,绘制得到降水量的折线图,如下图所示.

(1)求这![]() 天的平均降水量;
天的平均降水量;
(2)根据降水量的折线图,分别估计该工程施工延误天数![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某支教队有8名老师,现欲从中随机选出2名老师参加志愿活动,
(1)若规定选出的至少有一名女老师,则共有18种不同的需安排方案,试求该支教队男、女老师的人数;
(2)在(1)的条件下,记![]() 为选出的2位老师中女老师的人数,写出
为选出的2位老师中女老师的人数,写出![]() 的分布列.
的分布列.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com