
����Ŀ����ͼ,��֪��λԲx2+y2=1��x�������ύ�ڵ�P,��Բ��һ����Q��P��������ʱ�뷽����תһ�ܻص�P���ֹͣ�˶���OQɨ�������ζ�Ӧ��Բ�Ľ�Ϊxrad,��0<x<2��ʱ,��Բ��O��ֱ��PQ�ľ���Ϊy,y��x�ĺ�����ϵʽy=f(x)����ͼ��ʾ�ij����ͼ�еĢ٢�������ϵʽ
(��)д�������ͼ�Т٢ڴ��ĺ�����ϵʽ;
(��)�������yֵΪ2,���Q������.
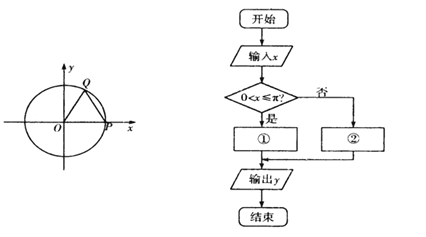
���𰸡�(1)������;(2)������.
�������������������1����������õ���������ʽΪf(x)= ��������һ�����ɵõ��������2����0<x<2
��������һ�����ɵõ��������2����0<x<2![]() ʱx=
ʱx=![]() ��
��![]() <x<2
<x<2![]() ʱ, x=
ʱ, x=![]() ���ֱ���õ������.
���ֱ���õ������.
������
(I)��0<x�ܦ�ʱ,y=cos![]() ;,
;,
����<x<2��ʱ,y=cos(��-![]() )=-cos
)=-cos![]()
���Ͽ�֪,��������ʽΪf(x)= .
.
���Կ�ͼ�Т٢ڴ�Ӧ����ʽ�ӷֱ�Ϊy=cos![]() ,y=-cos
,y=-cos![]() ,
,
(��)�������yֵΪ,��
��0<x<2![]() ʱ��cos
ʱ��cos![]() =
=![]() ,��x=
,��x=![]() ,��ʱ��Q������Ϊ(-
,��ʱ��Q������Ϊ(-![]() ,
,![]() ;
;
��![]() <x<2
<x<2![]() ʱ,��-cos=
ʱ,��-cos=![]() =
=![]() ,��x=
,��x=![]() ,��ʱ��Q������Ϊ(-
,��ʱ��Q������Ϊ(-![]() ,-
,-![]() ).
).



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������f��x��=Asin��x+�գ���A��0��0����4��|��|�� ![]() �����㣨0��
�����㣨0�� ![]() �����ҵ�x=
�����ҵ�x= ![]() ʱ������f��x��ȡ�����ֵ1��
ʱ������f��x��ȡ�����ֵ1��
��1��������f��x����ͼ������ƽ�� ![]() ����λ�õ�����g��x��������g��x���ı���ʽ��
����λ�õ�����g��x��������g��x���ı���ʽ��
��2���ڣ�1���������£�����h��x��=f��x��+g��x��+2cos2x��1���������x1 �� x2��R������h��x1����h��x����h��x2������|x1��x2|����Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ֱ�ΪP��1��0����Q��2��0����R��4��0����S��8��0���ĸ������һ��ֱ�ߣ���������ֱ��ǡΧ�������Σ���������ε����������Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ������ϵxOy�У���OΪ���㣬x��������Ϊ���Ὠ��������ϵ��ֱ��l�ļ����귽��Ϊ��sin����+ ![]() ��=
��= ![]() ��ԲO�IJ�������Ϊ
��ԲO�IJ�������Ϊ  ����Ϊ������r��0����
����������r��0����
������ԲO��Բ�ĵļ����꣨�ѡ�0��0�ܦȣ�2�� ����
����rΪ��ֵʱ��ԲO�ϵĵ㵽ֱ��l��������Ϊ2+ ![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������R�ϵ��溯��f��x������x��0ʱ��
f��x��= ��
��
�����x�ĺ���F��x��=f��x����a��0��a��1�����������֮��Ϊ��������
A.1��2a
B.2a��1
C.1��2��a
D.2��a��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������S��ABC�У�SB�͵���ABC����SB=AB=2��BC= ![]() ��D��E�ֱ���SA��SC���е㣮
��D��E�ֱ���SA��SC���е㣮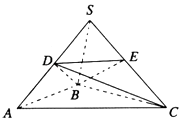
��I����֤��ƽ��ACD��ƽ��BCD��
��II��������S��BD��E��ƽ��ǵĴ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���躯��f�䣨x�����溯��f��x����x��R���ĵ�������f����1��=0����x��0ʱ��xf�䣨x����f��x����0����ʹ��f��x����0������x��ȡֵ��Χ�ǣ� ��
A.�����ޣ���1���ȣ�0��1��
B.����1��0���ȣ�1��+�ޣ�
C.�����ޣ���1���ȣ���1��0��
D.��0��1���ȣ�1��+�ޣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ax3+3x2+1�������ٴ�������ʵ��m��ʹ��f����m����f��1����f��m+2���ɵȲ����У��������ԭ��������y=f��x�������߿������� ��
A.3��
B.2��
C.1��
D.0��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У���֪ ![]() ��sinB=cosAsinC��S��ABC=6��PΪ�߶�AB�ϵĵ㣬��
��sinB=cosAsinC��S��ABC=6��PΪ�߶�AB�ϵĵ㣬��  ����xy�����ֵΪ ��
����xy�����ֵΪ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com