
已知函数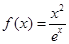 .
.
(1)求函数 的单调区间;
的单调区间;
(2)若方程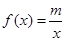 有解,求实数m的取值范围;
有解,求实数m的取值范围;
(3)若存在实数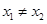 ,使
,使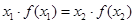 成立,求证:
成立,求证: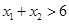 .
.
(1) 递增区间为
递增区间为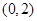 ,递减区间为
,递减区间为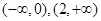 ;(2)
;(2)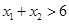 ;(3)详见解析.
;(3)详见解析.
解析试题分析:(1)对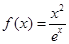 求导可得
求导可得 ,令
,令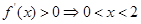 ,
,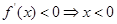 或
或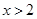 ,由导数与单调性的关系可知,所以
,由导数与单调性的关系可知,所以 递增区间为
递增区间为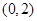 ,递减区间为
,递减区间为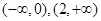 ;
;
(2)若方程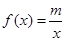 有解
有解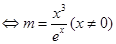 有解,令
有解,令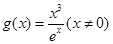 ,则原问题转化为求g(x)的值域,而m只要再g(x)的值域内即可。故对g(x)求导,则
,则原问题转化为求g(x)的值域,而m只要再g(x)的值域内即可。故对g(x)求导,则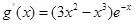 令
令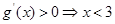 ,
,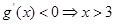 ,所以
,所以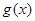 在
在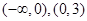 递增,在
递增,在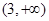 递减,
递减, ,故
,故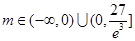 ;
;
(3)根据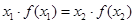 的结构,构造辅助函数
的结构,构造辅助函数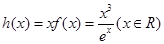 ,则由(2)知,
,则由(2)知, 在
在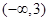 递增,在
递增,在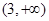 递减,由条件有
递减,由条件有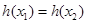 ,不妨设
,不妨设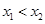 ,则必有
,则必有 ,于是
,于是 ,再利用反证法证明,假设
,再利用反证法证明,假设 ,则
,则 ,
,
即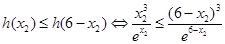
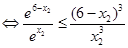 ,令
,令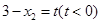 ,则有
,则有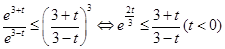 ,即
,即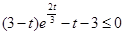 (*),、令
(*),、令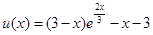
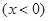 .
.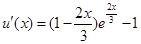 ,因为
,因为 恒成立,所以
恒成立,所以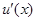 在
在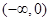 上是增函数,所以
上是增函数,所以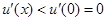 ,所以
,所以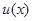 在
在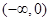 上是减函数,故
上是减函数,故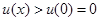 ,
,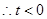 时,
时,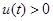 ,这与(*)矛盾!所以原不等式得证,即
,这与(*)矛盾!所以原不等式得证,即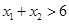 .
.
试题解析:解:(1) , 1分
, 1分
令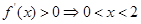 ,
,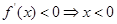 或
或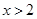 3分
3分
所以 递增区间为
递增区间为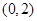 ,递减区间为
,递减区间为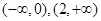 4分
4分
(2)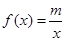
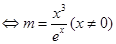 ,令
,令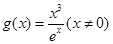 ,则
,则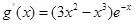
令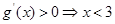 ,
,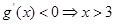 ,
,
所以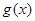 在
在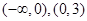 递增,在
递增,在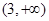 递减, 6分
递减, 6分 ,故
,故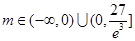 8分
8分
(3)令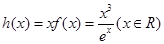 ,则由(2)知,
,则由(2)知, 在
在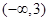 递增,在
递增,在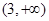 递减.
递减.
由条件有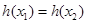 ,不妨设
,不妨设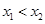 ,则必有
,则必有 ,于是
,于是


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:高中数学 来源: 题型:解答题
已知函数f(x)=x-aln x(a∈R).
(1)当a=2时,求曲线y=f(x)在点A(1,f(1))处的切线方程;
(2)求函数f(x)的极值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=x2-(1+2a)x+aln x(a为常数).
(1)当a=-1时,求曲线y=f(x)在x=1处切线的方程;
(2)当a>0时,讨论函数y=f(x)在区间(0,1)上的单调性,并写出相应的单调区间.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数f(x)=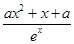 .
.
(1)函数f(x)在点(0,f(0))的切线与直线2x+y-1=0平行,求a的值;
(2)当x∈[0,2]时,f(x)≥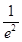 恒成立,求a的取值范围.
恒成立,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知f(x)=xln x,g(x)=x3+ax2-x+2.
(1)求函数f(x)的单调区间;
(2)求f(x)在区间[t,t+2](t>0)上的最小值;
(3)对一切的x∈(0,+∞),2f(x)<g′(x)+2恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
设函数f(x)=(x+1)ln x-2x.
(1)求函数的单调区间;
(2)设h(x)=f′(x)+ ,若h(x)>k(k∈Z)恒成立,求k的最大值.
,若h(x)>k(k∈Z)恒成立,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com