分析:(Ⅰ)由图读出A,最高点到时左边第一个零点的横坐标的差的绝对值为四分之一周期,求出周期T,进而求出ω,代入点的坐标求出φ,得f(x)的解析式;
(Ⅱ)由(Ⅰ)知f(x)的解析式,把x-
代入求f(x-
),进而求出g(x),利用降幂公式得一个角一个三角函数值,由x的范围,求出3x+
的范围,借助余弦函数的图象,求出cos(3x+
)的范围,进一步求出最大值.
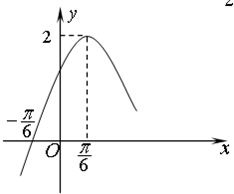
解答:解:(Ⅰ)由图知A=2,
=,则
=4×∴
ω=∴f(x)=2sin(
x+φ),∴2sin(
×
+φ)=2,
∴sin(
+φ)=1,∴
+φ=
,∴φ=
,
∴f(x)的解析式为
f(x)=2sin(x+)(Ⅱ)由(Ⅰ)可知:
f(x-)=2sin[(x-)+]=2sin(x+)∴
g(x)=[f(x-)]2=4×=2-2cos(3x+)∵
x∈[-,]∴
-<3x+<∴当
3x+=π即
x=时,g(x)
max=4
点评:给出条件求y=Asin(ωx+φ)的解析式,条件不管以何种方式给出,一般先求A,再求ω,最后求φ;求三角函数最值时,一般要把式子化为y=Asin(ωx+φ)+B或y=Acos(ωx+φ)+B的形式,从x的范围由里向外扩,一直扩到Asin(ωx+φ)+B或Acos(ωx+φ)+B的范围,即函数f(x)的值域,数形结合,看ωx+φ为多少时,取得最值.用到转化化归的思想.

 函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<
函数f(x)=Asin(ωx+φ)(x∈R,A>0,ω>0,0<φ<

 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|< 当x∈[-
当x∈[- 函数f(x)=Asin(ωx+φ),x∈R(A>0,ω>0,|φ|<
函数f(x)=Asin(ωx+φ),x∈R(A>0,ω>0,|φ|<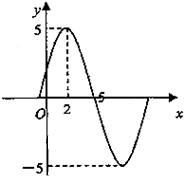 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R,|φ|<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,x∈R,|φ|<