
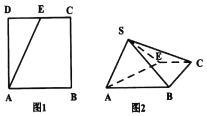
【题目】如图,点E为正方形ABCD边CD上异于点C、D的动点,将△ADE沿AE翻折成△SAE,在翻折过程中,下列三个说法中正确的个数是( )
①存在点E和某一翻折位置使得AE∥平面SBC;
②存在点E和某一翻折位置使得SA⊥平面SBC;
③二面角S﹣AB﹣E的平面角总是小于2∠SAE.
A.0B.1C.2D.3
【答案】B
【解析】
对于①,四边形ABCE为梯形,所以AE与BC必然相交;对于②,假设SA![]() 平面SBC,可推得矛盾;对于③,当将△ADE沿AE翻折使得平面SAE⊥平面ABCE时,二面角S﹣AB﹣E最大,在平面SAE内,作出一个角等于二面角S﹣AB﹣E的平面角;由角
平面SBC,可推得矛盾;对于③,当将△ADE沿AE翻折使得平面SAE⊥平面ABCE时,二面角S﹣AB﹣E最大,在平面SAE内,作出一个角等于二面角S﹣AB﹣E的平面角;由角![]() 所在三角形的一个外角,它是不相邻的两个内角之和,结合图形,即可判定③.
所在三角形的一个外角,它是不相邻的两个内角之和,结合图形,即可判定③.
对于①,四边形ABCE为梯形,所以AE与BC必然相交,故①错误;
对于②,假设SA![]() 平面SBC,SC
平面SBC,SC![]() 平面SBC,所以SA⊥SC,又SA⊥SE,SE∩SC=S,所以SA⊥平面SCE,所以平面SCE∥平面SBC,这与平面SBC∩平面SCE=SC矛盾,
平面SBC,所以SA⊥SC,又SA⊥SE,SE∩SC=S,所以SA⊥平面SCE,所以平面SCE∥平面SBC,这与平面SBC∩平面SCE=SC矛盾,
故假设不成立,即②错误;
对于③,当将△ADE沿AE翻折使得平面SAE⊥平面ABCE时,二面角S﹣AB﹣E最大,如图,在平面SAE内,作SO⊥AE,垂足为O,∴SO⊥平面ABCE;AB![]() 平面ABCE,
平面ABCE,
所以SO⊥AB;
作OF⊥AB,垂足为F,连接SF,SO∩OF=O,则AB⊥平面SFO,所以AB⊥SF,则∠SFG即为二面角S﹣AB﹣E的平面角;
在直线AE上取一点![]() ,使得O
,使得O![]() =OF,连接S
=OF,连接S![]() ,则∠S
,则∠S![]() O=∠SFO;
O=∠SFO;
由图形知,在△SA![]() 中,S
中,S![]() >A
>A![]() ,所以∠AS
,所以∠AS![]() <∠SAE;而∠S
<∠SAE;而∠S![]() O=∠SAE+∠AS
O=∠SAE+∠AS![]() ,
,
故∠S![]() O<2∠SAE;
O<2∠SAE;
即∠SFO<2∠SAE.故③正确.
故选:B.


科目:高中数学 来源: 题型:
【题目】若数列![]() 同时满足条件:①存在互异的
同时满足条件:①存在互异的![]() 使得
使得![]() (
(![]() 为常数);
为常数);
②当![]() 且
且![]() 时,对任意
时,对任意![]() 都有
都有![]() ,则称数列
,则称数列![]() 为双底数列.
为双底数列.
(1)判断以下数列![]() 是否为双底数列(只需写出结论不必证明);
是否为双底数列(只需写出结论不必证明);
①![]() ; ②
; ②![]() ; ③
; ③![]()
(2)设![]() ,若数列
,若数列![]() 是双底数列,求实数
是双底数列,求实数![]() 的值以及数列
的值以及数列![]() 的前
的前![]() 项和
项和![]() ;
;
(3)设![]() ,是否存在整数
,是否存在整数![]() ,使得数列
,使得数列![]() 为双底数列?若存在,求出所有的
为双底数列?若存在,求出所有的![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某中学2018年的高考考生人数是2015年高考考生人数的![]() 倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:
倍,为了更好地对比该校考生的升学情况,统计了该校2015年和2018年的高考情况,得到如图柱状图:

则下列结论正确的是![]()
![]()
A. 与2015年相比,2018年一本达线人数减少
B. 与2015年相比,2018年二本达线人数增加了![]() 倍
倍
C. 2015年与2018年艺体达线人数相同
D. 与2015年相比,2018年不上线的人数有所增加
查看答案和解析>>
科目:高中数学 来源: 题型:
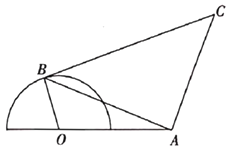
【题目】某生态农庄有一块如图所示的空地,其中半圆O的直径为300米,A为直径延长线上的点,![]() 米,B为半圆上任意一点,以AB为一边作等腰直角
米,B为半圆上任意一点,以AB为一边作等腰直角![]() ,其中BC为斜边.
,其中BC为斜边.
![]() 若
若![]() ;,求四边形OACB的面积;
;,求四边形OACB的面积;
![]() 现决定对四边形OACB区域地块进行开发,将
现决定对四边形OACB区域地块进行开发,将![]() 区域开发成垂钓中心,预计每平方米获利10元,将
区域开发成垂钓中心,预计每平方米获利10元,将![]() 区域开发成亲子采摘中心,预计每平方米获利20元,则当
区域开发成亲子采摘中心,预计每平方米获利20元,则当![]() 为多大时,垂钓中心和亲子采摘中心获利之和最大?
为多大时,垂钓中心和亲子采摘中心获利之和最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
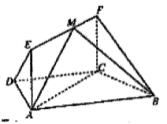
【题目】如图,在四边形![]() 中,
中,![]() ,
,![]() ,四边形
,四边形![]() 为矩形,且
为矩形,且![]() 平面
平面![]() ,
,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)点![]() 在线段
在线段![]() 上运动,当点
上运动,当点![]() 在什么位置时,平面
在什么位置时,平面![]() 与平面
与平面![]() 所成锐二面角最大,并求此时二面角的余弦值.
所成锐二面角最大,并求此时二面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知四棱锥S﹣ABCD的底面为矩形,SA⊥底面ABCD,点E在线段BC上,以AD为直径的圆过点 E.若SA=![]() AB=3,则△SED面积的最小值为_____.
AB=3,则△SED面积的最小值为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com