
【题目】已知函数![]() ,
,![]() .
.
![]() 求证:
求证:![]() 对
对![]() 恒成立;
恒成立;
![]() 若
若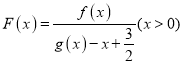 ,若
,若![]() ,
,![]() ,求证:
,求证:![]()
【答案】(1)证明见解析(2)证明见解析
【解析】
(1)先对不等式左边进行化简整理,然后将整理后的表达式设为函数![]() ,对函数
,对函数![]() 进行一阶导数和二阶导数的分析,得到
进行一阶导数和二阶导数的分析,得到![]() 在
在![]() 上单调递增,则当
上单调递增,则当![]() 时,
时,![]() 命题得证.
命题得证.
(2)先对整理后的![]() 进行一阶导数的分析,画出函数
进行一阶导数的分析,画出函数![]() 大致图象,可知
大致图象,可知![]() ,
,![]() 然后采用先取对数然后作差的方法比较大小,关键是构造对数平均数,利用对数平均不等式即可证明.
然后采用先取对数然后作差的方法比较大小,关键是构造对数平均数,利用对数平均不等式即可证明.
证明:![]() 由题意,可知
由题意,可知
![]() .
.
令![]() ,
,![]() 则
则
![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增.
上单调递增.
![]() 当
当![]() 时,
时,![]() ,
,
![]() 在
在![]() 上单调递增.
上单调递增.
![]() 当
当![]() 时,
时,![]() .
.
故命题得证.
![]() 由题意,
由题意,![]() ,
,![]() .
.
![]() ,
,![]() .
.
![]() 令
令![]() ,解得
,解得![]() ;
;
![]() 令
令![]() ,解得
,解得![]() ;
;
![]() 令
令![]() ,解得
,解得![]() .
.
![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
在![]() 处取得极小值
处取得极小值![]() .
.
![]() 大致图象如下:
大致图象如下:
根据图,可知![]() ,
,![]() .
.
![]()
![]() ,
,![]() ,
,
![]() 根据对数平均不等式,有
根据对数平均不等式,有
![]() ,
,
![]() .
.
![]() ,
,
![]() .
.
![]()
故得证.


科目:高中数学 来源: 题型:
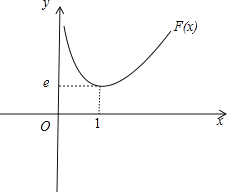
【题目】已知椭圆![]() :
:![]() 过点
过点 ,且以
,且以![]() ,
,![]()
![]() 为焦点,椭圆
为焦点,椭圆![]() 的离心率为
的离心率为![]() .
.
(1)求实数![]() 的值;
的值;
(2)过左焦点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,
两点,![]() 为坐标原点,问椭圆
为坐标原点,问椭圆![]() 上是否存在点
上是否存在点![]() ,使线段
,使线段![]() 和线段
和线段![]() 相互平分?若存在,求出点
相互平分?若存在,求出点![]() 的坐标,若不存在,说明理由。
的坐标,若不存在,说明理由。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设椭圆![]() ,离心率
,离心率![]() ,短轴
,短轴![]() ,抛物线顶点在原点,以坐标轴为对称轴,焦点为
,抛物线顶点在原点,以坐标轴为对称轴,焦点为![]() ,
,
(1)求椭圆和抛物线的方程;
(2)设坐标原点为![]() ,
,![]() 为抛物线上第一象限内的点,
为抛物线上第一象限内的点,![]() 为椭圆是一点,且有
为椭圆是一点,且有![]() ,当线段
,当线段![]() 的中点在
的中点在![]() 轴上时,求直线
轴上时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
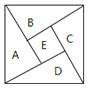
【题目】如图为我国数学家赵爽![]() 约3世纪初
约3世纪初![]() 在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则
在为《周髀算经》作注时验证勾股定理的示意图,现在提供5种颜色给其中5个小区域涂色,规定每个区域只涂一种颜色,相邻区域颜色不同,则![]() 区域涂色不相同的概率为
区域涂色不相同的概率为![]()
![]()
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在三棱锥![]() 中,底面是边长为
中,底面是边长为![]() 的正三角形,点
的正三角形,点![]() 在底面
在底面![]() 上的射影
上的射影![]() 恰是
恰是![]() 的中点,侧棱
的中点,侧棱![]() 和底面成
和底面成![]() 角.
角.
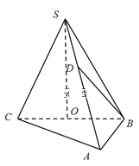
(1)若![]() 为侧棱
为侧棱![]() 上一点,当
上一点,当![]() 为何值时,
为何值时,![]() ;
;
(2)求二面角![]() 的余弦值大小.
的余弦值大小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,点E为正方形ABCD边CD上异于点C、D的动点,将△ADE沿AE翻折成△SAE,在翻折过程中,下列三个说法中正确的个数是( )
①存在点E和某一翻折位置使得AE∥平面SBC;
②存在点E和某一翻折位置使得SA⊥平面SBC;
③二面角S﹣AB﹣E的平面角总是小于2∠SAE.
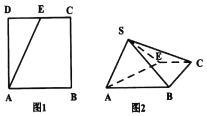
A.0B.1C.2D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现定义:设![]() 是非零实常数,若对于任意的
是非零实常数,若对于任意的![]() ,都有
,都有![]() ,则称函数
,则称函数![]() 为“关于的
为“关于的![]() 偶型函数”
偶型函数”
(1)请以三角函数为例,写出一个“关于2的偶型函数”的解析式,并给予证明
(2)设定义域为的“关于的![]() 偶型函数”在区间
偶型函数”在区间![]() 上单调递增,求证在区间
上单调递增,求证在区间![]() 上单调递减
上单调递减
(3)设定义域为![]() 的“关于
的“关于![]() 的偶型函数”
的偶型函数”![]() 是奇函数,若
是奇函数,若![]() ,请猜测
,请猜测![]() 的值,并用数学归纳法证明你的结论
的值,并用数学归纳法证明你的结论
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】谢尔宾斯基三角形(Sierpinski triangle)是一种分形几何图形,由波兰数学家谢尔宾斯基在1915年提出,它是一个自相似的例子,其构造方法是:
(1)取一个实心的等边三角形(图1);
(2)沿三边中点的连线,将它分成四个小三角形;
(3)挖去中间的那一个小三角形(图2);
(4)对其余三个小三角形重复(1)(2)(3)(4)(图3).
制作出来的图形如图4,….
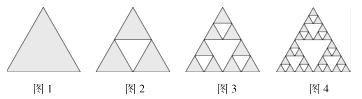
若图1(阴影部分)的面积为1,则图4(阴影部分)的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com