
| A. | f(x)=1,g(x)=x0 | B. | f(x)=x,g(x)=$\sqrt{{x}^{2}}$ | C. | f(x)=x,g(x)=($\sqrt{{x}^{2}}$)2 | D. | f(x)=|x|,g(t)=$\sqrt{{t}^{2}}$ |
分析 可通过求f(x),g(x)的定义域,以及比较f(x),g(x)的对应法则,从而可判断f(x),g(x)是否为同一函数,从而找出正确选项.
解答 解:A.f(x)的定义域为R,g(x)的定义域为{x|x≠0},∴f(x),g(x)不是同一函数;
B.f(x)=x,$g(x)=\sqrt{{x}^{2}}=|x|$,对应法则不同不是同一函数;
C.$f(x)=x,g(x)=(\sqrt{{x}^{2}})^{2}={x}^{2}$,对应法则不同,不是同一函数;
D.$f(x)=|x|,g(t)=\sqrt{{t}^{2}}=|t|$,定义域和对应法则都相同,是同一函数.
故选D.
点评 考查两函数为同一函数的概念及判断方法,函数定义域的求法,知道由定义域和对应法则可以确定一个函数.


 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案科目:高中数学 来源: 题型:选择题
| A. | (-$\frac{1}{2014}$,-$\frac{1}{2015}$]∪[$\frac{1}{2015}$,$\frac{1}{2014}$) | B. | (-$\frac{1}{2014}$,-$\frac{1}{2015}$)∪($\frac{1}{2015}$,$\frac{1}{2014}$) | ||
| C. | (-$\frac{1}{2013}$,-$\frac{1}{2014}$]∪[$\frac{1}{2016}$,$\frac{1}{2015}$) | D. | (-$\frac{1}{2014}$,-$\frac{1}{2015}$]∪[$\frac{1}{2016}$,$\frac{1}{2015}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y-2=0 | B. | x-y+3=0 | C. | x+y-3=0 | D. | x-y+2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{32}$ | B. | $\frac{1}{16}$ | C. | $\frac{1}{64}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
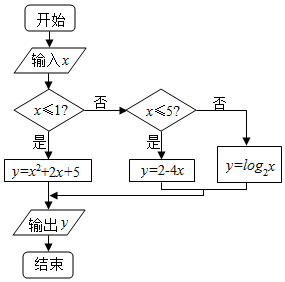
| A. | 2 | B. | ${log_2}\frac{π}{2}$ | C. | 2-2π | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | n | B. | 2 | C. | 2n | D. | $\frac{n}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com