
分析 (1)由已知可得:$\left\{\begin{array}{l}\frac{1}{2}×2c×b=\sqrt{3}\\ e=\frac{c}{a}=\frac{\sqrt{3}}{2}\\{a}^{2}={b}^{2}+{c}^{2}\end{array}\right.$,解得a2,b2的值,可得椭圆方程;
(2)由(1)可得A2(2,0),F1(-$\sqrt{3}$,0),分MN的斜率不存在和MN的斜率存在两种情况,分析△MA2N的面积最大值,及相应的k值,可得答案.
解答 解:(1)由已知可得:
$\left\{\begin{array}{l}\frac{1}{2}×2c×b=\sqrt{3}\\ e=\frac{c}{a}=\frac{\sqrt{3}}{2}\\{a}^{2}={b}^{2}+{c}^{2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{a}^{2}=4\\{b}^{2}=1\\{c}^{2}=3\end{array}\right.$,
∴椭圆方程为:$\frac{{x}^{2}}{4}+{y}^{2}=1$…(5分);
(2)由(1)可得:A2(2,0),F1(-$\sqrt{3}$,0),
当MN的斜率不存在时,
|MN|=1,△MA2N的面积S=1+$\frac{\sqrt{3}}{2}$
当MN的斜率存在时,设MN的方程为:y=k(x+$\sqrt{3}$),
代入$\frac{{x}^{2}}{4}+{y}^{2}=1$得:(${k}^{2}+\frac{1}{4}$)x2+$2\sqrt{3}{k}^{2}$x+3k2-1=0,
设M(x1,y1),N(x2,y2)则:
则x1+x2=$\frac{-2\sqrt{3}{k}^{2}}{{k}^{2}+\frac{1}{4}}$,x1x2=$\frac{3{k}^{2}-1}{{k}^{2}+\frac{1}{4}}$…(8分);
|y1-y2|=|k(x1+$\sqrt{3}$)-k(x2+$\sqrt{3}$)|=|k||x1-x2|=|k|$\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{\left|k\right|\sqrt{{k}^{2}+1}}{{k}^{2}+\frac{1}{4}}$,
令t=${k}^{2}+\frac{1}{4}$,(t≥$\frac{1}{4}$),
则|y1-y2|=$\frac{\sqrt{(t-\frac{1}{4})(t+\frac{3}{4})}}{t}$=$\sqrt{-\frac{3}{16}(\frac{1}{t})^{2}+\frac{1}{2}•\frac{1}{t}+1}$,
令u=$\frac{1}{t}$,则u∈(0,4]
则当u=$\frac{4}{3}$时,|y1-y2|取最大值$\frac{2\sqrt{3}}{3}$>1,此时k=±$\frac{\sqrt{2}}{2}$,
此时△MA2N的面积取最大值1+$\frac{2\sqrt{3}}{3}$,
此时MN的方程为:y=±$\frac{\sqrt{2}}{2}$(x+$\sqrt{3}$).
点评 本题考查的知识点是椭圆的标准方程,椭圆的性质,直线与椭圆的位置关系,分类讨论思想,难度中档.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | $±\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
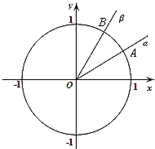 如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A,B两点.
如图,在平面直角坐标系中,锐角α,β的终边分别与单位圆交于A,B两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $({0,\sqrt{2}})$ | B. | $({0,\sqrt{3}})$ | C. | $({\sqrt{2},\sqrt{3}})$ | D. | $({\sqrt{3},2})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com