
分析 先根据题意可知AB=BP,BC=CP进而根据余弦定理可求得cos2θ的值进而求得θ,最后在直角三角形PCD中求得答案
解答 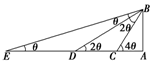 解:如图所示,△BED,△BDC为等腰三角形,BD=ED=600,BC=DC=200$\sqrt{3}$.
解:如图所示,△BED,△BDC为等腰三角形,BD=ED=600,BC=DC=200$\sqrt{3}$.
在△BCD中,由余弦定理可得cos2θ=$\frac{60{0}^{2}+(200\sqrt{3})^{2}-(200\sqrt{3})^{2}}{2×600×200\sqrt{3}}$=$\frac{\sqrt{3}}{2}$,
所以2θ=30°,4θ=60°.
在Rt△ABC中,AB=BC•sin 4θ=200$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=300(cm).
点评 本题考查利用数学知识解决实际问题,考查余弦定理的运用,考查学生分析解决问题的能力,属于中档题.


科目:高中数学 来源: 题型:解答题
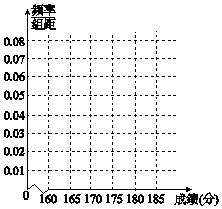 某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表:
某高校在2011年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表:| 组号 | 分组 | 频数 | 频率 |
| 第1组 | [160,165) | 5 | 0.05 |
| 第2组 | [165,170) | ① | 0.35 |
| 第3组 | [170,175) | 30 | ② |
| 第4组 | [175,180) | 20 | 0.20 |
| 第5组 | [180,185] | 10 | 0.10 |
| 合计 | 100 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|0<x≤3} | B. | {x|1≤x≤3} | C. | {x|0≤x≤3} | D. | {x|1<x≤3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{5}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com