
【题目】已知函数![]() 有两个极值点.
有两个极值点.
(1)求实数![]() 的范围;
的范围;
(2)设函数![]() 的两个极值点分别为
的两个极值点分别为![]() ,
,![]() ,且
,且![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:
【题目】约公元前600年,几何学家泰勒斯第一个测出了金字塔的高度.如图,金字塔是正四棱锥,泰勒斯先测量出某个金字塔的底棱长约为230米;然后,他站立在沙地上,请人不断测量他的影子,当他的影子和身高相等时,他立刻测量出该金字塔影子的顶点A与相应底棱中点B的距离约为22.2米.此时,影子的顶点A和底面中心O的连线恰好与相应的底棱垂直,则该金字塔的高度约为( )
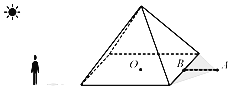
A.115米B.137.2米C.230米D.252.2米
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校高中三个年级共有4000人,为了了解各年级学周末在家的学习情况,现通过分层抽样的方法获得相关数据如下(单位:小时),其中高一学生周末的平均学习时间记为![]() .
.
高一:14 15 15.5 16.5 17 17 18 19
高二:15 16 16 16 17 17 18.5
高三:16 17 18 21.5 24
(1)求每个年级的学生人数;
(2)从高三被抽查的同学中随机抽取2人,求2人学习时间均超过![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() ,
, ![]() ,函数
,函数![]() ,
, ![]() .
.
(Ⅰ)若![]() 与
与![]() 有公共点
有公共点![]() ,且在
,且在![]() 点处切线相同,求该切线方程;
点处切线相同,求该切线方程;
(Ⅱ)若函数![]() 有极值但无零点,求实数
有极值但无零点,求实数![]() 的取值范围;
的取值范围;
(Ⅲ)当![]() ,
, ![]() 时,求
时,求![]() 在区间
在区间![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 对任意的
对任意的![]() ,均有
,均有![]() ,则称函数
,则称函数![]() 具有性质
具有性质![]() .
.
(1)判断下面两个函数是否具有性质![]() ,并说明理由.①
,并说明理由.①![]() ;②
;②![]() .
.
(2)若函数![]() 具有性质
具有性质![]() ,且
,且![]() ,求证:对任意
,求证:对任意![]() 有
有![]() ;
;
(3)在(2)的条件下,是否对任意![]() 均有
均有![]() .若成立给出证明,若不成立给出反例.
.若成立给出证明,若不成立给出反例.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】第18届国际篮联篮球世界杯(世界男子篮球锦标赛更名为篮球世界杯后的第二届世界杯)于2019年8月31日至9月15日在中国的北京、广州、南京、上海、武汉、深圳、佛山、东莞八座城市举行.中国队12名球员在第一场和第二场得分的茎叶图如图所示,则下列说法错误的是( )
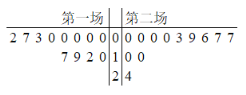
A.第一场得分的中位数为![]() B.第二场得分的平均数为
B.第二场得分的平均数为![]()
C.第一场得分的极差大于第二场得分的极差D.第一场与第二场得分的众数相等
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两位同学各有![]() 张卡片,现以投掷一枚骰子的形式进行游戏,当掷出奇数点时.甲赢得乙卡片一张,当掷出偶数点时,乙赢得甲卡片一张.规定投掷的次数达到
张卡片,现以投掷一枚骰子的形式进行游戏,当掷出奇数点时.甲赢得乙卡片一张,当掷出偶数点时,乙赢得甲卡片一张.规定投掷的次数达到![]() 次,或在此之前某入赢得对方所有卡片时,游戏终止.
次,或在此之前某入赢得对方所有卡片时,游戏终止.
(1)设![]() 表示游戏终止时投掷的次数,求
表示游戏终止时投掷的次数,求![]() 的分布列及期望;
的分布列及期望;
(2)求在投掷![]() 次游戏才结束的条件下,甲、乙没有分出胜负的概率.
次游戏才结束的条件下,甲、乙没有分出胜负的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com